
【题目】盒中有6只灯泡,其中有2只是次品,4只是正品.从中任取2只,试求下列事件的概率.
(1)取到的2只都是次品;
(2)取到的2只中恰有一只次品.
【答案】
(1)解:将6只灯泡分别标号为1,2,3,4,5,6;且1,2为次品;
从6只灯泡中取出2只的基本事件:
1﹣2、1﹣3、1﹣4、1﹣5、1﹣6、2﹣3、2﹣4、2﹣5、2﹣6、3﹣4、3﹣5、3﹣6、4﹣5、4﹣6、5﹣6共有15种
从6只灯泡中取出2只都是次品的事件只有1个,因此取到2只次品的概率为 ![]() .
.
(2)解:根据题意,取到的2只产品中正品,次品各一只的事件有
1﹣3、1﹣4、1﹣5、1﹣6、2﹣3、2﹣4、2﹣5、2﹣6共有8种,
而总的基本事件共有15种,
因此取到2只产品中恰有一只次品的概率为 ![]() .
.
【解析】(1)将6只灯泡分别标号为1,2,3,4,5,6;且1,2为次品;用列举法可得从6只灯泡中取出2只的基本事件,即可得从6只灯泡中取出2只都是次品的事件只有1个,进而由等可能事件的概率计算可得答案;(2)由(1)所的基本事件,分析可得取到的2只产品中正品,次品各一只的事件数目,由古典概型概率公式,计算可得答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】对某地区儿童的身高与体重的一组数据,我们用两种模型①![]() ,②
,②![]() 拟合,得到回归方程分别为
拟合,得到回归方程分别为![]() ,
, ![]() ,作残差分析,如表:
,作残差分析,如表:
身高 | 60 | 70 | 80 | 90 | 100 | 110 |
体重 | 6 | 8 | 10 | 14 | 15 | 18 |
| 0.41 | 0.01 | 1.21 | -0.19 | 0.41 | |
| -0.36 | 0.07 | 0.12 | 1.69 | -0.34 | -1.12 |
(Ⅰ)求表中空格内的值;
(Ⅱ)根据残差比较模型①,②的拟合效果,决定选择哪个模型;
(Ⅲ)残差大于![]() 的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
(结果保留到小数点后两位)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为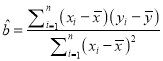 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】.某几何体如图所示, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是边长为
是边长为![]() 的正三角形,
的正三角形, ![]() ,
, ![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
(I)求证: ![]() 平面
平面![]() .
.
(II)求证:平面![]() 平面
平面![]() .
.
(III)求该几何体的体积.
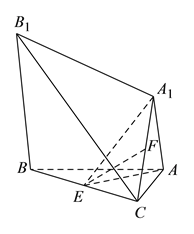
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,棱柱ABC﹣A1B1C1的侧面BCC1B1是菱形,B1C⊥A1B 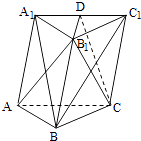
(1)证明:平面AB1C⊥平面A1BC1;
(2)设D是A1C1上的点,且A1B∥平面B1CD,求A1D:DC1的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体![]() 的棱长为
的棱长为![]() ,
,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,过直线
的中点,过直线![]() ,
,![]() 的平面分别与棱
的平面分别与棱![]() 、
、![]() 交于
交于![]() ,
,![]() ,设
,设![]() ,
,![]() ,给出以下四个命题:
,给出以下四个命题:
①平面![]() 平面
平面![]() ;
;
②当且仅当![]() 时,四边形
时,四边形![]() 的面积最小;
的面积最小;
③四边形![]() 周长
周长![]() ,
,![]() 是单调函数;
是单调函数;
④四棱锥![]() 的体积
的体积![]() 为常函数;
为常函数;
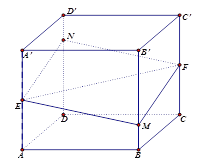
以上命题中假命题的序号为( ).
A. ①④ B. ② C. ③ D. ③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是某公交公司1路车从起点站A站途经B站和C站,最终到达终点站D站的格点站路线图.(8×8的格点图是由边长为1的小正方形组成)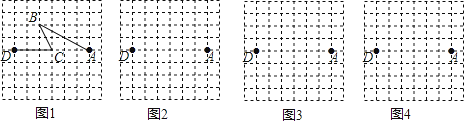
(1)求1路车从A站到D站所走的路程(精确到0.1);
(2)在图2、图3和图4的网格中各画出一种从A站到D站的路线图.(要求:①与图1路线不同、路程相同;②途中必须经过两个格点站;③所画路线图不重复)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com