
分析 (1)设点C(x,y),由AC,BC所在直线的斜率之积等于m(m≠0),分类讨论,即可求顶点C的轨迹E的方程,并判断轨迹E为何种圆锥曲线;
((2)当m=-$\frac{1}{2}$时,曲线E的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1(x≠0)$.设直线l:y=kx+b,(k≠0,b≠0),A(x1,y1),B(x2,y2),M(xM,yM),联立直线方程与椭圆方程,通过韦达定理求解KOM,然后推出直线OM的斜率与l的斜率的乘积为定值.
解答 解:(1)设点C(x,y),由AC,BC所在直线的斜率之积等于m(m≠0),
得:$\frac{y-1}{x}•\frac{y+1}{x}$=m,化简得:-mx2+y2=1(x≠0).
当m<-1时,轨迹E表示焦点在y轴上的椭圆,且除去(0,1),(0,-1)两点;
当m=-1时,轨迹E表示以(0,0)为圆心,半径是1的圆,且除去(0,1),(0,-1)两点;
当-1<m<0时,轨迹E表示焦点在x轴上的椭圆,且除去(0,1),(0,-1)两点;
当m>0时,轨迹E表示焦点在y轴上的双曲线,且除去(0,1),(0,-1)两点.
(2)当m=-$\frac{1}{2}$时,曲线E的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1(x≠0)$.
设直线l:y=kx+b(k≠0,b≠0),A(x1,y1),B(x2,y2),M(xM,yM).
将y=kx+b代入$\frac{x^2}{8}+\frac{y^2}{4}=1$得(2k2+1)x2+4kbx+2b2-8=0
故${x_m}=\frac{{{x_1}+{x_2}}}{2}=\frac{-2kb}{{2{k^2}+1}},{y_m}=k•{x_m}+b=\frac{b}{{2{k^2}+1}}$
于是直线OM的斜率${k_{om}}=\frac{y_m}{x_m}=-\frac{1}{2k},即{k_{om}}.k=-\frac{1}{2}$
所以直线OM的斜率与直线l的斜率的乘积为定值.
点评 本题考查椭圆方程的综合应用,椭圆的方程的求法,考查分析问题解决问题的能力.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2x-2 | B. | y=log2x | C. | y=x2+1 | D. | y=x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
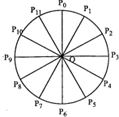 如图圆O是半径为1的圆,点PO、P1、P2…、P11将圆12等分,则$\overrightarrow{O{P}_{0}}$$•\overrightarrow{O{P}_{i}}$(i=0,1,2,3,…,11)的取值集合是{-1,-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,0,$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,1}.
如图圆O是半径为1的圆,点PO、P1、P2…、P11将圆12等分,则$\overrightarrow{O{P}_{0}}$$•\overrightarrow{O{P}_{i}}$(i=0,1,2,3,…,11)的取值集合是{-1,-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,0,$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$,1}.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com