
【题目】若对任意x∈(0,π),不等式ex﹣e﹣x>asinx恒成立,则实数a的取值范围是( )
A.[﹣2,2]
B.(﹣∞,e]
C.(﹣∞,2]
D.(﹣∞,1]
【答案】C
【解析】解:令f(x)=ex﹣e﹣x﹣asinx, 当a≤0时,∵x∈(0,π),∴ex>e﹣x , sinx>0,∴ex﹣e﹣x>0,﹣asinx≥0,∴f(x)>0;
当a>0时,f′(x)=ex+e﹣x﹣acosx,
①若0<a≤2,∵x∈(0,π),∴ex+e﹣x>2,acosx<a≤2,f′(x)>0,∴f(x)在(0,π)上单调递增,∴f(x)>f(0)=0,满足题意;
②若a>2时,f′(0)=2﹣a<0,f′( ![]() )>0,∴存在x0∈(0,
)>0,∴存在x0∈(0, ![]() ),使得f′(x0)=0.
),使得f′(x0)=0.
令g(x)=ex+e﹣x﹣acosx,∵g′(x)=ex﹣e﹣x+asinx在(0, ![]() )上单调递增,∴g′(x)>g′(0)=0,
)上单调递增,∴g′(x)>g′(0)=0,
∴g(x)=f′(x)=ex+e﹣x﹣acosx在(0, ![]() )上单调递增,∴x∈(0,x0)时,f′(x)<0,f(x)在(0,x0)上单调递减,
)上单调递增,∴x∈(0,x0)时,f′(x)<0,f(x)在(0,x0)上单调递减,
∴f(x)<f(0)=0不满足题意.
综上所述,a∈(﹣∞,2],
故选:C.


科目:高中数学 来源: 题型:
【题目】高一(1)班参加校生物竞赛学生的成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:

(1)求高一(1)班参加校生物竞赛的人数及分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(2)若要从分数在[80,100]之间的学生中任选2人进行某项研究,求至少有1人分数在[90,100]之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,己知曲线C1 的方程为ρ=2cosθ+2sinθ,直线 C2 的参数方程为![]() (t 为参数)
(t 为参数)
(Ⅰ)将 C1 的方程化为直角坐标方程;
(Ⅱ)P 为 C1 上一动点,求 P 到直线 C2 的距离的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴,建立极坐标系,若直线l的参数方程为 ![]() (t为参数,α为l的倾斜角),曲线E的极坐标方程为ρ=4sinθ.射线θ=β,θ=β+
(t为参数,α为l的倾斜角),曲线E的极坐标方程为ρ=4sinθ.射线θ=β,θ=β+ ![]() ,θ=β﹣
,θ=β﹣ ![]() 与曲线E分别交于不同于极点的三点A、B、C.
与曲线E分别交于不同于极点的三点A、B、C.
(1)求证:|OB|+|OC|= ![]() |OA|;
|OA|;
(2)当β= ![]() 时,直线l过B、C两点,求y0与α的值.
时,直线l过B、C两点,求y0与α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
:![]() ,圆
,圆![]() :
:![]() ,动点
,动点![]() 在直线
在直线![]() :
:![]() 上(
上(![]() ),过
),过![]() 分别作圆
分别作圆![]() ,
,![]() 的切线,切点分别为
的切线,切点分别为![]() ,
,![]() ,若满足
,若满足![]() 的点
的点![]() 有且只有一个,则实数
有且只有一个,则实数![]() 的值为______.
的值为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,等腰梯形ABCD的底角A等于60°.直角梯形ADEF所在的平面垂直于平面 ABCD,∠EDA=90°,且ED=AD=2AF=2AB=2.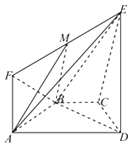
(Ⅰ)证明:平面ABE⊥平面EBD;
(Ⅱ)点M在线段EF上,试确定点M的位置,使平面MAB与平面ECD所成的角的余弦值为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于下列说法正确的是( )
A.若f(x)是奇函数,则f(x)是单调函数
B.命题“若x2﹣x﹣2=0,则x=1”的逆否命题是“若x≠1,则x2﹣x﹣2=0”
C.命题p:?x∈R,2x>1024,则¬p:?x0∈R, ![]()
D.命题“?x∈(﹣∞,0),2x<x2”是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图长方体![]() 中,
中,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 的中点
的中点

(1)求证:平面![]() 平面
平面![]() ;
;
(2)请在答题卡图形中画出直线![]() 与平面
与平面![]() 的交点
的交点![]() (保留必要的辅助线),写出画法并计算
(保留必要的辅助线),写出画法并计算![]() 的值(不必写出计算过程).
的值(不必写出计算过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com