
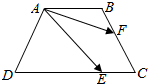
 如图,已知ABCD是底角为60°的等腰梯形,其中AB∥CD,AD=4,DC=6,$\overrightarrow{DE}$=2$\overrightarrow{EC}$,$\overrightarrow{CF}$=2$\overrightarrow{FB}$,则$\overrightarrow{AE}$•$\overrightarrow{AF}$的值为$\frac{28}{3}$.
如图,已知ABCD是底角为60°的等腰梯形,其中AB∥CD,AD=4,DC=6,$\overrightarrow{DE}$=2$\overrightarrow{EC}$,$\overrightarrow{CF}$=2$\overrightarrow{FB}$,则$\overrightarrow{AE}$•$\overrightarrow{AF}$的值为$\frac{28}{3}$. 分析 由题意求出AB,然后利用共线向量基本定理把$\overrightarrow{AE}$、$\overrightarrow{AF}$用梯形四边所在向量表示,展开后代入数量积公式得答案.
解答  解:如图,∵ABCD是底角为60°的等腰梯形,AB∥CD,AD=4,DC=6,
解:如图,∵ABCD是底角为60°的等腰梯形,AB∥CD,AD=4,DC=6,
∴可求得AB=2.
又$\overrightarrow{AE}=\overrightarrow{AD}+\overrightarrow{DE}=-\overrightarrow{DA}+\frac{2}{3}\overrightarrow{DC}$,$\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{BF}$=$\overrightarrow{AB}+\frac{1}{3}\overrightarrow{BC}$,
∴$\overrightarrow{AE}$•$\overrightarrow{AF}$=$(-\overrightarrow{DA}+\frac{2}{3}\overrightarrow{DC})•(\overrightarrow{AB}+\frac{1}{3}\overrightarrow{BC})$
=$-\overrightarrow{DA}•\overrightarrow{AB}-\frac{1}{3}\overrightarrow{DA}•\overrightarrow{BC}+\frac{2}{3}\overrightarrow{DC}•\overrightarrow{AB}+\frac{2}{9}\overrightarrow{DC}•\overrightarrow{BC}$
=$-4×2×cos60°-\frac{1}{3}×4×4×cos120°$$+\frac{2}{3}×6×2×cos0°+\frac{2}{9}×6×4×cos60°$
=$-4+\frac{8}{3}+\frac{24}{3}+\frac{8}{3}=\frac{28}{3}$.
故答案为:$\frac{28}{3}$.
点评 本题考查平面向量的数量积运算,考查了向量的加法与减法的三角形法则,是中档题.


科目:高中数学 来源: 题型:解答题
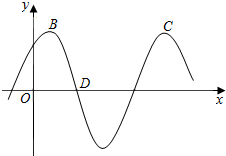 如图所示,B,C两点是函数f(x)=Asin(2x+$\frac{π}{3}$)(A>0)图象上相邻的两个最高点,D点为函数f(x)图象与x轴的一个交点.
如图所示,B,C两点是函数f(x)=Asin(2x+$\frac{π}{3}$)(A>0)图象上相邻的两个最高点,D点为函数f(x)图象与x轴的一个交点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (0,2) | C. | (-$\frac{1}{9}$,$\frac{19}{9}$) | D. | (-$\frac{1}{5}$,$\frac{9}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(b-3)<f(a+2) | B. | f(b-3)>f(a+2) | ||
| C. | f(b-3)=f(a+2) | D. | f(b-3)与f(a+2)的大小无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{8}$ | D. | $\frac{3}{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com