
【题目】已知函数![]() 且
且![]() .
.
(Ⅰ) 若1是关于x的方程![]() 的一个解,求t的值;
的一个解,求t的值;
(Ⅱ) 当![]() 且
且![]() 时,解不等式
时,解不等式![]() ;
;
(Ⅲ)若函数![]() 在区间(-1,2]上有零点,求t的取值范围.
在区间(-1,2]上有零点,求t的取值范围.
【答案】(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]() (Ⅲ)
(Ⅲ) ![]() 或
或![]()
【解析】
试题分析:(Ⅰ)由![]() ,即可求得
,即可求得![]() 的值;
的值;
(Ⅱ)当![]() 时,当
时,当![]() 时,
时,![]() 即
即![]() ,利用对数函数的单调性可得真数间的大小关系,注意对数函数的定义域;
,利用对数函数的单调性可得真数间的大小关系,注意对数函数的定义域;
(Ⅲ)分情况讨论:若![]() ,则
,则![]() 在
在![]() 上没有零点,当
上没有零点,当![]() 时,分
时,分![]() 在
在![]() 内有重根
内有重根![]() ,则△=0,解得
,则△=0,解得![]() 的值;
的值;![]() 在
在![]() 上只有一个零点,且不是方程的重根时;
上只有一个零点,且不是方程的重根时;![]() 在
在![]() 上有两个相异实根三种情况,根据函数零点判定定理可得不等式,解出即可;
上有两个相异实根三种情况,根据函数零点判定定理可得不等式,解出即可;
试题解析:(Ⅰ)∵若1是关于![]() 的方程
的方程![]() 的解,
的解, ![]() ,又
,又![]() .
.
(Ⅱ) ![]() 时,
时,![]() ,又
,又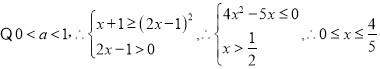 ,∴解集为:
,∴解集为:![]() ;
;
(Ⅲ)若![]() ,则
,则![]() 在
在![]() 上没有零点.下面就
上没有零点.下面就![]() 时分三种情况讨论:方程
时分三种情况讨论:方程![]() 在
在![]() 上有重根
上有重根![]() ,则
,则![]() ,解得
,解得![]() ;①
;①
![]() 在
在![]() 上只有一个零点,且不是方程的重根,则有
上只有一个零点,且不是方程的重根,则有![]() ,解得
,解得![]() ,又经检验:
,又经检验:![]() 时,
时,![]() 在
在![]() 上都有零点,
上都有零点,![]() .②;
.②;![]() 在
在![]() 上有两个相异实根,则有:
上有两个相异实根,则有:
 或
或 ,解得
,解得![]() ,③;综合①②③可知
,③;综合①②③可知![]() 的取值范围为
的取值范围为![]() 或
或![]()


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为 ![]() 与p,且乙投球2次均未命中的概率为
与p,且乙投球2次均未命中的概率为 ![]() .
.
(Ⅰ)求乙投球的命中率p;
(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在![]() 上的函数
上的函数![]() (
(![]() ,
, ![]() ),给出以下四个论断:
),给出以下四个论断:
①![]() 的周期为
的周期为![]() ;②
;②![]() 在区间
在区间![]() 上是增函数;③
上是增函数;③![]() 的图象关于点
的图象关于点![]() 对称;④
对称;④![]() 的图象关于直线
的图象关于直线![]() 对称.以其中两个论断作为条件,另两个论断作为结论,写出你认为正确的一个命题(写成“
对称.以其中两个论断作为条件,另两个论断作为结论,写出你认为正确的一个命题(写成“![]() ”的形式)__________.(其中用到的论断都用序号表示)
”的形式)__________.(其中用到的论断都用序号表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“累积净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示.根据GB/T18801﹣2015《空气净化器》国家标准,对空气净化器的累积净化量(CCM)有如下等级划分:
累积净化量(克) | (3,5] | (5,8] | (8,12] | 12以上 |
等级 | P1 | P2 | P3 | P4 |
为了了解一批空气净化器(共2000台)的质量,随机抽取n台机器作为样本进行估计,已知这n台机器的
累积净化量都分布在区间(4,14]中,按照(4,6],(6,8],(8,10],(10,12],(12,14],均匀分组,其中累积净化量在(4,6]的所有数据有:4.5,4.6,5.2,5.7和5.9,并绘制了如下频率分布直方图.
(Ⅰ)求n的值及频率分布直方图中的x值;
(Ⅱ)以样本估计总体,试估计这批空气净化器(共2000台)中等级为P2的空气净化器有多少台?
(Ⅲ)从累积净化量在(4,6]的样本中随机抽取2台,求恰好有1台等级为P2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数集X={x1,x2,…,xn}(其中xi>0,i=1,2,…,n,n≥3),若对任意的xk∈X(k=1,2,…,n),都存在xi,xj∈X(xi≠xj),使得下列三组向量中恰有一组共线:
①向量(xi,xk)与向量(xk,xj);②向量(xi,xj)与向量(xj,xk);③向量(xk,xi)与向量(xi,xj),则称X具有性质P。例如{1,2,4}具有性质P。
(1)若{1,3,x)具有性质P,则x的取值为________;
(2)若数集{1,3,x1,x2}具有性质P,则x1+x2的最大值与最小值之积为________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某某车站在春运期间为了改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位:min).下面是这次抽样的频率分布表和频率分布直方图,解答下列问题:
分组 | 频数 | 频率 | |
一组 | 0≤t<5 | 0 | 0 |
二组 | 5≤t<10 | 10 | |
三组 | 10≤t<15 | 10 | 0.10 |
四组 | 15≤t<20 | ||
五组 | 20≤t<25 | 30 | 0.30 |
合计 | 100 | 1.00 | |

(1)这次抽样的样本容量是多少?
(2)在表中填写缺失的数据并补全频率分布直方图.
(3)旅客购票用时的平均数可能落在哪一个小组?
(4)若每增加一个购票窗口可使平均购票用时缩短5 min,要使平均购票用时不超过10 min,那么你估计最少要增加几个窗口?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第![]() 个家庭的月收入
个家庭的月收入![]() (单位:千元)与月储蓄
(单位:千元)与月储蓄![]() (单位:千元)的数据资料,算得
(单位:千元)的数据资料,算得![]() ,
, ![]() ,
,
![]() ,
, ![]()
(1).求家庭的月储蓄![]() 对月收入
对月收入![]() 的线性回归方程
的线性回归方程![]() ;
;
(2).判断变量![]() 与
与![]() 之间的正相关还是负相关;
之间的正相关还是负相关;
(3).若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:回归直线的斜率和截距的最小二乘估计公式分别为

![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com