
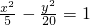 ;
;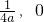 );
);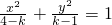 不可能表示椭圆.
不可能表示椭圆. 得
得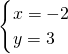 ,故①正确;②中根据渐近线方程求得a和b的关系,进而根据焦距求得a和b,双曲线方程可得,判断②正确;③把抛物线方程整理成标准方程,进而根据抛物线的性质可得抛物线的焦点在y轴上,判断③错误;④当4-k>0,k-1>0且4-k≠k-1时,曲线表示椭圆,故④错误.
,故①正确;②中根据渐近线方程求得a和b的关系,进而根据焦距求得a和b,双曲线方程可得,判断②正确;③把抛物线方程整理成标准方程,进而根据抛物线的性质可得抛物线的焦点在y轴上,判断③错误;④当4-k>0,k-1>0且4-k≠k-1时,曲线表示椭圆,故④错误. 得
得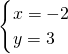 ,
, =2,a2+b2=25求得a=
=2,a2+b2=25求得a= ,b=2
,b=2 ,故可知结论②正确;
,故可知结论②正确; y,根据抛物线性质可知,抛物线的焦点在y轴上,故③错误;
y,根据抛物线性质可知,抛物线的焦点在y轴上,故③错误;

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
| 8 |
| 9 |
| 7 |
| 6 |
| 1 |
| 3 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省文登市高三上学期期中统考理科数学试卷(解析版) 题型:选择题
给出下列四个命题,其错误的是( )
①已知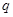 是等比数列
是等比数列 的公比,则“数列
的公比,则“数列 是递增数列”是“
是递增数列”是“ ”的既不充分也不必要条件;
”的既不充分也不必要条件;
②若定义在 上的函数
上的函数 是奇函数,则对定义域内的任意
是奇函数,则对定义域内的任意 必有
必有 ;
;
③若存在正常数 满足
满足 ,则
,则 的一个正周期为
的一个正周期为 ;
;
④函数 与
与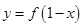 图像关于
图像关于 对称.
对称.
A.②④ B.④ C.③ D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com