已知函数
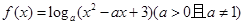
满足:对任意实数
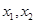
,当
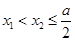
时,总有
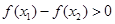
,则实数
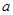
的取值范围是( )
试题分析:据题意,不等式
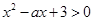
恒成立,所以
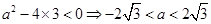
.
又当
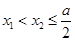
时,总有
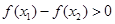
,结合对数函数与二次函数的单调性知
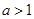
.综上得
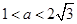
.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已函数
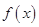
是定义在
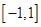
上的奇函数,在
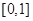
上时
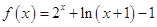
(Ⅰ)求函数
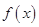
的解析式;
(Ⅱ)解不等式
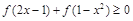
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
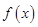
是定义域为
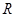
的单调减函数,且是奇函数,当
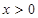
时,
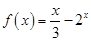
(1)求
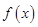
的解析式;(2)解关于
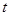
的不等式
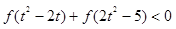
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设
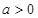
,
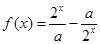
是
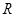
上的奇函数.
(Ⅰ)求
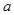
的值;
(Ⅱ)证明:
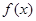
在
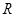
上为增函数;
(Ⅲ)解不等式:
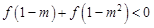
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
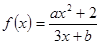
是奇函数,且
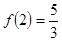
.
(1)求实数
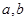
的值;
(2)判断函数
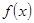
在
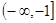
上的单调性,并用定义加以证明.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
定义在
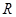
上的函数
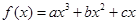
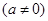
的单调增区间为
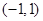
,若方程
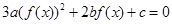
恰有4个不同的实根,则实数
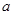
的值为( )
A.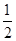 | B.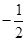 | C.1 | D.-1 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设
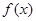
是定义在R上的奇函数,且当
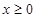
时,
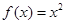
,若对任意的
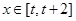
,不等式
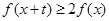
恒成立,则实数
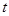
的取值范围是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
函数
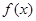
对任意
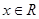
满足
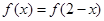
,且
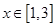
时
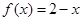
,则下列不等式一定成立的是( )
查看答案和解析>>

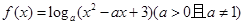 满足:对任意实数
满足:对任意实数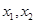 ,当
,当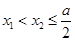 时,总有
时,总有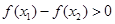 ,则实数
,则实数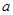 的取值范围是( )
的取值范围是( )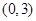
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案