
【题目】已知定义在R上的偶函数f(x)满足f(x+1)=﹣f(x),且当x∈[﹣1,0]时, ![]() ,函数
,函数 ![]() ,则关于x的不等式f(x)<g(x)的解集为( )
,则关于x的不等式f(x)<g(x)的解集为( )
A.(﹣2,﹣1)∪(﹣1,0)
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:由题意知,f(x+1)=﹣f(x),
∴f(x+2)=﹣f(x+1)=f(x),
即函数f(x)是周期为2的周期函数.
若x∈[0,1]时,﹣x∈[﹣1,0],
∵当x∈[﹣1,0]时, ![]() ,
,
∴当x∈[0,1]时, ![]() ,
,
∵f(x)是偶函数,∴f(x)= ![]() ,
,
即f(x)= 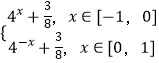 .
.
∵函数 ![]() ,
,
∴g(x)= 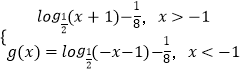 ,
,
作出函数f(x)和g(x)的图象如图:
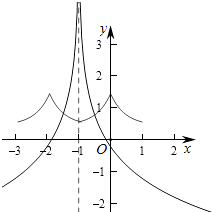
当﹣1<x<0时,由 ![]() =
= ![]() ,
,
则 ![]() ,由选项验证解得x=
,由选项验证解得x= ![]() ,
,
即此时不等式式f(x)<g(|x+1|)的解为﹣1<x< ![]() ,
,
∵函数g(x)关于x=﹣1对称,
∴不等式式f(x)<g(x)的解为﹣1<x< ![]() 或
或 ![]() <x<﹣1,
<x<﹣1,
即不等式的解集为( ![]() ,﹣1)∪(﹣1,
,﹣1)∪(﹣1, ![]() ),
),
故选:D.
【考点精析】本题主要考查了奇偶性与单调性的综合的相关知识点,需要掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性才能正确解答此题.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,满足下列条件的有两个的是( )
A.![]()
B.![]()
C.a=1,b=2,c=3
D.a=3,b=2,A=60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A1B1C1D1 , O是底面ABCD对角线的交点.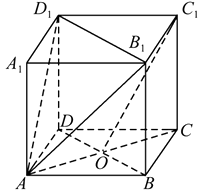
求证:(I) C1O∥面AB1D1;
(II)面A1C⊥面AB1D1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是公比不为1的等比数列,a1=1,且a1 , a3 , a2成等差数列.
(1)求数列{an}的通项;
(2)若数列{an}的前n项和为Sn , 试求Sn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx+φ), ![]() 的最小正周期为π,且图象关于x=
的最小正周期为π,且图象关于x= ![]() 对称.
对称.
(1)求ω和φ的值;
(2)将函数f(x)的图象上所有横坐标伸长到原来的4倍,再向右平移 ![]() 个单位得到函数g(x)的图象,求g(x)的单调递增区间以及g(x)≥1的x取值范围.
个单位得到函数g(x)的图象,求g(x)的单调递增区间以及g(x)≥1的x取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)为R上的偶函数,g(x)为R上的奇函数,且f(x)+g(x)=log4(4x+1).
(1)求f(x),g(x)的解析式;
(2)若函数h(x)=f(x)﹣ ![]() 在R上只有一个零点,求实数a的取值范围.
在R上只有一个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2, ![]() .
.
(1)若△ABC的面积等于 ![]() ,求a,b;
,求a,b;
(2)若sinB=2sinA,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com