
 为等差数列,其公差d不为0,
为等差数列,其公差d不为0, 和
和 的等差中项为11,且
的等差中项为11,且 ,令
,令 ,数列
,数列 的前n项和为
的前n项和为 .
. 及
及 ;
; 成等比数列?若存在,求出所有的m,n的值;若不存在,请说明理由.
成等比数列?若存在,求出所有的m,n的值;若不存在,请说明理由. ,
, ;(2)
;(2) .
. 和
和 的等差中项为11,转化为
的等差中项为11,转化为 ,与已知联立,利用等差数列的通项公式展开,解方程组得出基本量
,与已知联立,利用等差数列的通项公式展开,解方程组得出基本量 和
和 ,从而求出等差数列的通项公式,将
,从而求出等差数列的通项公式,将 代入到
代入到 中,利用裂项相消法求和;第二问,先假设存在m和n,利用已知看能不能求出m和n的值,利用第一问的结论
中,利用裂项相消法求和;第二问,先假设存在m和n,利用已知看能不能求出m和n的值,利用第一问的结论 ,得出
,得出 的值,由已知
的值,由已知 成等比数列,则
成等比数列,则 ,整理得到关于m,n的方程,通过解方程得出m和n的值.
,整理得到关于m,n的方程,通过解方程得出m和n的值. 为等差数列,公差为
为等差数列,公差为 ,则由题意得
,则由题意得

 3分
3分
 6分
6分 ,所以
,所以
 成等比,则有
成等比,则有 8分
8分 ,(1)
,(1)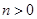 ,所以
,所以 , 10分
, 10分 ,当
,当 时,代入(1)式,得
时,代入(1)式,得 ;
; 可以使
可以使 成等比数列。 12分
成等比数列。 12分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的 ,都有
,都有
 为常数,且
为常数,且 .
. 是等比数列;
是等比数列; 的公比
的公比 ,数列
,数列 满足
满足
 ,
,
 ,求数列
,求数列 的通项公式;
的通项公式; 的前
的前 项和
项和 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 级需要的天数为
级需要的天数为 ,
,| 等级 | 等级图标 | 需要天数 | 等级 | 等级图标 | 需要天数 |
| 1 |  | 5 | 7 |     | 77 |
| 2 |   | 12 | 8 |   | 96 |
| 3 |    | 21 | 12 |    | 192 |
| 4 |  | 32 | 16 |  | 320 |
| 5 |   | 45 | 32 |   | 1152 |
| 6 |    | 60 | 48 |    | 2496 |
 级需要的天数
级需要的天数 __________
__________查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com