练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设等差数列{an}满足a3=5，a10=﹣9． （Ⅰ）求{an}的通项公式；
    （Ⅱ）求{an}的前n项和Sn及使得Sn最大的序号n的值．

    【答案】解：（Ⅰ）由an=a1+（n﹣1）d及a3=5，a10=﹣9得 a1+9d=﹣9，a1+2d=5
    解得d=﹣2，a1=9，
    数列{an}的通项公式为an=11﹣2n
    （Ⅱ）由（1）知Sn=na1+ d=10n﹣n2 ．
    因为Sn=﹣（n﹣5）2+25．
    所以n=5时，Sn取得最大值
    【解析】（1）设出首项和公差，根据a3=5，a10=﹣9，列出关于首项和公差的二元一次方程组，解方程组得到首项和公差，写出通项．（2）由上面得到的首项和公差，写出数列{an}的前n项和，整理成关于n的一元二次函数，二次项为负数求出最值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某营养学家建议：高中生每天的蛋白质摄入量控制在[60，90]（单位：克），脂肪的摄入量控制在[18，27]（单位：克）．某学校食堂提供的伙食以食物A和食物B为主，1千克食物A含蛋白质60克，含脂肪9克，售价20元；1千克食物B含蛋白质30克，含脂肪27克，售价15元． （Ⅰ）如果某学生只吃食物A，判断他的伙食是否符合营养学家的建议，并说明理由；
    （Ⅱ）为了花费最低且符合营养学家的建议，学生需要每天同时食用食物A和食物B各多少千克？并求出最低需要花费的钱数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】国家规定个人稿费纳税方法为：不超过800元的不纳税，超过800且不超过4000元的按超过800元的部分14%纳税，超过4000元的按全部稿费的11%纳税，
    （1）试根据上述规定建立某人所得稿费x元与纳税额y元的函数关系；
    （2）某人出了一本书，获得20000元的个人稿费，则这个人需要纳税是多少元？
    （3）某人发表一篇文章共纳税70元，则这个人的稿费是多少元？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数y= 的图象大致是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2+ax+b（a，b∈R）． （Ⅰ）已知x∈[0，1]
    （i）若a=b=1，求函数f（x）的值域；
    （ii）若函数f（x）的值域为[0，1]，求a，b的值；
    （Ⅱ）当|x|≥2时，恒有f（x）≥0，且f（x）在区间（2，3]上的最大值为1，求a2+b2的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中， ， ，且△ABC的周长为 ．
    （1）求点A的轨迹方程C；
    （2）过点P（2，1）作曲线C的一条弦，使弦被这点平分，求此弦所在的直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】平面直角坐标系xOy中，过椭圆M： （a＞b＞0）右焦点的直线x+y﹣ =0交M于A，B两点，P为AB的中点，且OP的斜率为 ． （Ⅰ）求M的方程
    （Ⅱ）C，D为M上的两点，若四边形ACBD的对角线CD⊥AB，求四边形ACBD面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，E为PA的中点，F为BC的中点，底面ABCD是菱形，对角线AC，BD交于点O．求证：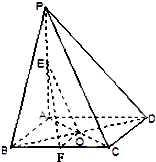

    （1）平面EFO∥平面PCD；
    （2）平面PAC⊥平面PBD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列{an}是首项为0的递增数列，fn（x）=|sin （x﹣an）|，x∈[an ， an+1]，n∈N* ， 满足：对于任意的b∈[0，1），fn（x）=b总有两个不同的根，则{an}的通项公式为

    查看答案和解析>>

    同步练习册答案