
 的正视图和侧视图均是直角三角形,俯视图为矩形,N、F分别是SC、AB的中点,
的正视图和侧视图均是直角三角形,俯视图为矩形,N、F分别是SC、AB的中点,  ,
, .
.
 ∴
∴ -------(3分)
-------(3分)

 平面SAD FN
平面SAD FN 平面SAD ∴NF∥平面SAD------(7分)
平面SAD ∴NF∥平面SAD------(7分) 点为原点,
点为原点, 所在直线为
所在直线为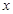 轴,
轴, 所在直线为
所在直线为 轴,SA所在直线为
轴,SA所在直线为 轴的空间直角坐标系,如图所示.
轴的空间直角坐标系,如图所示.
 ,
, ,
, ,
, ,
, 如下图所示.
如下图所示. ------------------…(9分)
------------------…(9分) ,
,
 --------------(10分)
--------------(10分)

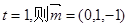 ----------------------------------------(11分)
----------------------------------------(11分) 的法向量
的法向量 ,则
,则 ,
, 即
即

 ,则
,则 ------------------------------ (12分)
------------------------------ (12分)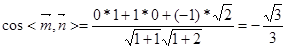 ------------ (13分)
------------ (13分) 是钝角二面角
是钝角二面角 的余弦值为
的余弦值为 ......................................................... (14分)
......................................................... (14分)

科目:高中数学 来源:不详 题型:解答题
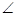 ABC=60
ABC=60 ,E
,E C
C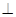 面ABCD,FA
面ABCD,FA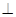 面ABCD,G
面ABCD,G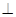 面ABF
面ABF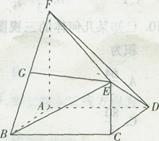
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com