
分析 (Ⅰ)由题意,列方程组,求得a和b的值,即可求得椭圆方程;
(Ⅱ)求得K的横坐标,将直线方程代入椭圆方程,$\frac{|AK|}{|AE|}+\frac{|AK|}{|AF|}=|{x_A}-{x_k}|•(\frac{1}{{|{x_A}-{x_E}|}}+\;\frac{1}{{|{x_A}-{x_F}|}})$,利用韦达定理,即可求得t的值.
解答 解:(Ⅰ)由题意可知:$\left\{\begin{array}{l}e=\frac{c}{a}=\frac{{\sqrt{3}}}{2}\\ a=2\\{a^2}={b^2}+{c^2}\end{array}\right.$,解得:$\left\{\begin{array}{l}a=2\\ b=1\\ c=\sqrt{3}\end{array}\right.$,
∴椭圆C的方程为$\frac{x^2}{4}+{y^2}=1$. …(4分)
(Ⅱ) 设直线m的方程为y=kx+b,有b=2-2k.
解得点K的横坐标${x_K}=\frac{2-4b}{1+4k}$,…(5分)
将直线m代入椭圆方程得:(1+4k2)x2+8kbx+4b2-4=0,
由韦达定理,得${x_E}+{x_F}=\frac{-8kb}{{1+4{k^2}}}$,${x_E}{x_F}=\frac{{4{b^2}-4}}{{1+4{k^2}}}$,…(7分)
所以$\frac{|AK|}{|AE|}+\frac{|AK|}{|AF|}=|{x_A}-{x_k}|•(\frac{1}{{|{x_A}-{x_E}|}}+\;\frac{1}{{|{x_A}-{x_F}|}})$=$|2-\frac{2-4b}{1+4k}|•\frac{{|4-({x_F}+{x_E})|}}{{|4-2({x_F}+{x_E})+{x_F}{x_E}|}}$=$|\frac{8k+4b}{1+4k}|•\frac{{|4{k^2}+2bk+1|}}{{|4{k^2}+4bk+{b^2}|}}$=2.…(11分)
∴存在实数t=2,使得$\frac{1}{|AE|}+\frac{1}{|AF|}=\frac{t}{|AK|}$恒成立…(12分)
点评 本题考查椭圆的标准方程及简单几何性质,考查直线与椭圆的位置关系,韦达定理,弦长公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
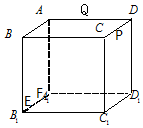 如图,正方体ABCD-A1B1C1D1的棱长为a(a>1),动点E,F在棱A1B1上,动点P,Q分别在棱CD,AD上,若EF=1,A1F=x,DP=y,DQ=z(x,y,z均大于零),则四面体PEFQ的体积( )
如图,正方体ABCD-A1B1C1D1的棱长为a(a>1),动点E,F在棱A1B1上,动点P,Q分别在棱CD,AD上,若EF=1,A1F=x,DP=y,DQ=z(x,y,z均大于零),则四面体PEFQ的体积( )| A. | 与x,y,z都有关 | B. | 与x有关,与y,z无关 | ||
| C. | 与y有关,与x,z无关 | D. | 与z有关,与x,y无关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α<β | B. | α>β | ||
| C. | α=β | D. | 无法确定α与β大小 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 模型1的相关指数R2为0.75 | B. | 模型2的相关指数R2为0.90 | ||
| C. | 模型3的相关指数R2为0.28 | D. | 模型4的相关指数R2为0.55 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com