
曲线![]() 与直线
与直线![]() 有两个交点时,实数k的取值范围是 ( )
有两个交点时,实数k的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 A【解析】析:要求的实数k的取值范围即为直线l斜率的取值范围,主要求出斜率的取值范围,方法为:曲线y=1+
A【解析】析:要求的实数k的取值范围即为直线l斜率的取值范围,主要求出斜率的取值范围,方法为:曲线y=1+ ![]() 表示以(0,1)为圆心,2为半径的半圆,在坐标系中画出相应的图形,直线l与半圆有不同的交点,故抓住两个关键点:当直线l与半圆相切时,圆心到直线的距离等于圆的半径,利用点到直线的距离公式列出关于k的方程,求出方程的解得到k的值;当直线l过B点时,由A和B的坐标求出此时直线l的斜率,根据两种情况求出的斜率得出k的取值范围.
表示以(0,1)为圆心,2为半径的半圆,在坐标系中画出相应的图形,直线l与半圆有不同的交点,故抓住两个关键点:当直线l与半圆相切时,圆心到直线的距离等于圆的半径,利用点到直线的距离公式列出关于k的方程,求出方程的解得到k的值;当直线l过B点时,由A和B的坐标求出此时直线l的斜率,根据两种情况求出的斜率得出k的取值范围.
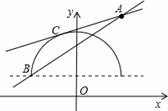
解答:解:根据题意画出图形,如图所示:
由题意可得:直线l过A(2,4),B(-2,1),
又直线y=1+![]() 图象为以(0,1)为圆心,2为半径的半圆,
图象为以(0,1)为圆心,2为半径的半圆,
当直线l与半圆相切,C为切点时,圆心到直线l的距离d=r,即![]() =2,解得:k=
=2,解得:k=![]() ;当直线l过B点时,直线l的斜率为
;当直线l过B点时,直线l的斜率为![]() =
=![]() ,
,
则直线l与半圆有两个不同的交点时,实数k的范围为(![]() ,
,![]() ].故答案为:A
].故答案为:A


科目:高中数学 来源:2011-2012学年河北省高三下学期二调考试文科数学试卷(解析版) 题型:填空题
给出以下四个结论:
(1)若关于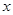 的方程
的方程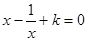 在
在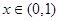 没有实数根,则
没有实数根,则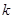 的取值范围是
的取值范围是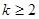
(2)曲线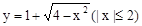 与直线
与直线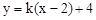 有两个交点时,实数
有两个交点时,实数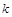 的取值范围是
的取值范围是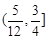
(3)已知点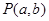 与点
与点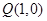 在直线
在直线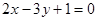 两侧, 则3b-2a>1;
两侧, 则3b-2a>1;
(4)若将函数 的图像向右平移
的图像向右平移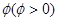 个单位后变为偶函数,则
个单位后变为偶函数,则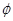 的最小值是
的最小值是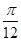 ;其中正确的结论是:__________________
;其中正确的结论是:__________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com