
【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE,设PA=1,AD=2.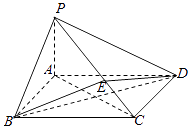
(1)求平面BPC的法向量;
(2)求二面角B﹣PC﹣A的正切值.
【答案】
(1)解:∵PA⊥平面ABCD,BD平面ABCD,
∴PA⊥BD.
∵PC⊥平面BDE,BD平面BDE,∴PC⊥BD.
又PA∩PC=P,∴BD⊥平面PAC,AC平面PAC,
∴BD⊥AC.
又底面ABCD为矩形,∴ABCD为正方形.
建立如图所示的空间直角坐标系.
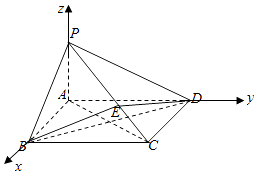
A(0,0,0),B(2,0,0),C(2,2,0),P(0,0,1),
D(0,2,0).
![]() =(0,2,0),
=(0,2,0), ![]() =(﹣2,0,1),
=(﹣2,0,1),
设平面BPC的法向量为 ![]() =(x,y,z),
=(x,y,z),
∴ 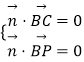 ,∴
,∴ ![]() ,取
,取 ![]() =(1,0,2).
=(1,0,2).
∴平面BPC的一个法向量为 ![]() =(1,0,2).
=(1,0,2).
(2)平面PAC的法向量为: ![]() =(﹣2,2,0).
=(﹣2,2,0).
设二面角B﹣PC﹣A=θ,由图可知:θ为锐角.
则cos ![]() =
= ![]() =
= ![]() =﹣
=﹣ ![]() .
.
∴cosθ= ![]() .
.
∴sinθ= ![]() .
.
∴tanθ= ![]() =3.即二面角B﹣PC﹣A的正切值为3.
=3.即二面角B﹣PC﹣A的正切值为3.
【解析】(1)先利用线面垂直的判定定理可证BD⊥平面PAC,进而可证BD⊥AC,从而可证ABCD为正方形,再建立空间直角坐标系,设平面BPC的法向量,利用平面向量的数量积等于0可得平面BPC的一个法向量;(2)先计算平面PAC的法向量,再设二面角B﹣PC﹣A=θ,可得cosθ,进而利用同角三角函数的基本关系可得tanθ,即二面角B﹣PC﹣A的正切值.
【考点精析】解答此题的关键在于理解平面的法向量的相关知识,掌握若向量![]() 所在直线垂直于平面
所在直线垂直于平面![]() ,则称这个向量垂直于平面
,则称这个向量垂直于平面![]() ,记作
,记作![]() ,如果
,如果![]() ,那么向量
,那么向量![]() 叫做平面
叫做平面![]() 的法向量.
的法向量.


科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为A,B,C所对边,a+b=4,(2﹣cosA)tan ![]() =sinA.
=sinA.
(1)求边长c的值;
(2)若E为AB的中点,求线段EC的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,体现了古代劳动人民的数学智慧,其中第六章“均输”中,有一竹节容量问题,某人根据这一思想,设计了如图所示的程序框图,若输出m的值为35,则输入的a的值为 . 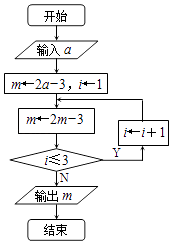
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,椭圆C: ![]() 的离心率是
的离心率是 ![]() ,
,
抛物线E:x2=4y的焦点F是C的一个顶点.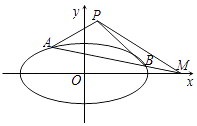
(1)求椭圆C的方程;
(2)设与坐标轴不重合的动直线l与C交于不同的两点A和B,与x轴交于点M,且 ![]() 满足kPA+kPB=2kPM , 试判断点M是否为定点?若是定点求出点M的坐标;若不是定点请说明理由.
满足kPA+kPB=2kPM , 试判断点M是否为定点?若是定点求出点M的坐标;若不是定点请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,已知平面PBC⊥平面ABC.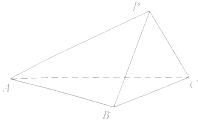
(1)若AB⊥BC,CP⊥PB,求证:CP⊥PA:
(2)若过点A作直线l⊥平面ABC,求证:l∥平面PBC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,已知平面AA1C1C⊥平面ABCD,且 ![]() ,AD=CD=1.
,AD=CD=1.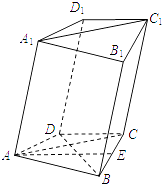
(1)求证:BD⊥AA1;
(2)若E为棱BC的中点,求证:AE∥平面DCC1D1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0),过点C(﹣4,0)作抛物线的两条切线CA,CB,A,B为切点,若直线AB经过抛物线y2=2px的焦点,△CAB的面积为24,则以直线AB为准线的抛物线标准方程是( )
A.y2=4x
B.y2=﹣4x
C.y2=8x
D.y2=﹣8x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com