练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某商场为提高服务质量，随机调查了50名男顾客和50名女顾客，每位顾客对该商场的服务给出满意或不满意的评价，得到下面列联表：

    满意

    不满意

    男顾客

    40

    10

    女顾客

    30

    20

    （1）分别估计男、女顾客对该商场服务满意的概率；

    （2）能否有95%的把握认为男、女顾客对该商场服务的评价有差异？

    附：．

    P（K2≥k）

    0.050

    0.010

    0.001

    k

    3.841

    6.635

    10.828

    【答案】（1）；

    （2）能有的把握认为男、女顾客对该商场服务的评价有差异.

    【解析】

    （1）从题中所给的列联表中读出相关的数据，利用满意的人数除以总的人数，分别算出相应的频率，即估计得出的概率值；

    （2）利用公式求得观测值与临界值比较，得到能有的把握认为男、女顾客对该商场服务的评价有差异.

    （1）由题中表格可知，50名男顾客对商场服务满意的有40人，

    所以男顾客对商场服务满意率估计为,

    50名女顾客对商场满意的有30人，

    所以女顾客对商场服务满意率估计为,

    （2）由列联表可知，

    所以能有的把握认为男、女顾客对该商场服务的评价有差异.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】函数的定义域为，且对任意，有，且当时，，

    (Ⅰ)证明是奇函数；

    (Ⅱ)证明在上是减函数；

    (III)若,，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在极坐标系中，直线的极坐标方程为，现以极点为原点，极轴为轴的非负半轴建立平面直角坐标系，曲线的参数方程为（为参数)．

    （1）求直线的直角坐标方程和曲线的普通方程；

    （2）若曲线为曲线关于直线的对称曲线，点分别为曲线、曲线上的动点，点坐标为，求的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P-ABCD中，PA⊥底面ABCD，AD∥BC，AB＝AD＝AC＝3，PA＝BC＝4，M为线段AD上一点，AM＝2MD，N为PC的中点.

    （Ⅰ）证明MN∥平面PAB；

    （Ⅱ）求四面体N-BCM的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国是世界上严重缺水的国家，某市为了制定合理的节水方案，对居民用水情况进行调查，通过抽样，获得某年100为居民每人的月均用水量（单位：吨），将数据按照分成9组，制成了如图所示的频率分布直方图.

    （1）求直方图的的值；

    （2）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，说明理由.

    （3）估计居民月用水量的中位数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知实数满足，若只在点（4，3）处取得最大值，则的取值范围是

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着机构改革的深入，各单位要减员增效，一家公司现有职员人（），且为偶数，每人每年可创利5万元，据评估，每裁员1人，留守职员每人每年多创利润0. 1万元，但公司要付下岗职员每人每年3万元的生活费.

    （1）假设公司裁员人，请写出公司获得的利益关于的解析式；

    （2）公司正常的运转所需人数不得少于现有职员的，为了获得最大效益，该公司应当裁员多少人.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设关于某产品的明星代言费（百万元）和其销售额（百万元），有如下表的统计表格：

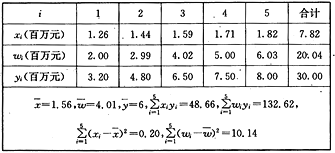
    表中

    （1）在给出的坐标系中，作出销售额关于广告费的回归方程的散点图，根据散点图指出：哪一个适合作销售额关于明星代言费的回归方程（不需要说明理由）；并求关于的回归方程（结果精确到0.1）

    （2）已知这种产品的纯收益（百万元）与，有如下关系：，用（1）中的结果估计当取何值时，纯收益取最大值？

    附：对于一组数据其回归线的斜率和截距的最小二乘估计分别为，

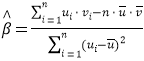    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下表为2015年至2018年某百货零售企业的年销售额（单位：万元）与年份代码的对应关系，其中年份代码年份-2014（如：代表年份为2015年）。

    年份代码

    1

    2

    3

    4

    年销售额

    105

    155

    240

    300

    （1）已知与具有线性相关关系，求关于的线性回归方程，并预测2019年该百货零售企业的年销售额；

    （2）2019年，美国为遏制我国的发展，又祭出“长臂管辖”的霸权行径，单方面发起对我国的贸易战，有不少人对我国经济发展前景表示担忧.此背景下，某调查平台为了解顾客对该百货零售企业的销售额能否持续增长的看法，随机调查了60为男顾客、50位女顾客，得到如下列联表：

    持乐观态度

    持不乐观态度

    总计

    男顾客

    45

    15

    60

    女顾客

    30

    20

    50

    总计

    75

    35

    110

    问：能否在犯错误的概率不超过0.05的前提下认为对该百货零售企业的年销售额持续增长所持的态度与性别有关？

    参考公式及数据：回归直线方程，

    0.10

    0.05

    0.025

    0.010

    0.005

    2.706

    3.841

    5.024

    6.635

    7.879

    查看答案和解析>>

    同步练习册答案