
分析 (1)根据极坐标方程和普通方程的关系即可转化为普通方程.
(2)根据直线和圆相交的位置关系结合弦长公式结合点到直线的距离公式进行求解即可.
解答 解:(1)由ρ2-6ρsinθ=-8.得x2+y2-6y=-8,
即x2+(y-3)2=1,
则圆M的直角坐标方程为x2+(y-3)2=1.
(2)直线l的参数方程为$\left\{\begin{array}{l}{x=-4t+a}\\{y=3t-1}\end{array}\right.$消去t得普通方程得3x+4y-3a+4=0,
∵直线l截圆M所得弦长为$\sqrt{3}$,
∴圆心(0,3)到直线l的距离d=$\frac{|16-3a|}{5}$=$\sqrt{1-(\frac{\sqrt{3}}{2})^{2}}$=$\frac{1}{2}$,
得a=$\frac{9}{2}$或a=$\frac{37}{6}$.
点评 本题主要考查极坐标和普通方程的关系的应用以及直线和圆相交的弦长公式的应用,考查学生的计算和转化能力.


科目:高中数学 来源: 题型:填空题
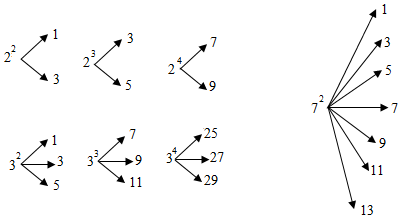 对于mn(m,n∈N且m,n≥2)可以按如下的方式进行“分解”,例如72的“分解“中最小的数是1,最大的数是13.若m3的“分解”中最小的数是111,则m=11.
对于mn(m,n∈N且m,n≥2)可以按如下的方式进行“分解”,例如72的“分解“中最小的数是1,最大的数是13.若m3的“分解”中最小的数是111,则m=11.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方形ABCD的边长为$\sqrt{2}$,且对角线AC的中点为O,E为AD的中点,将△ADC沿对角线AC折起得平面ADC⊥平面ABC.
如图,正方形ABCD的边长为$\sqrt{2}$,且对角线AC的中点为O,E为AD的中点,将△ADC沿对角线AC折起得平面ADC⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{3}{4}$,-$\frac{3}{5}$)∪($\frac{3}{5}$,$\frac{3}{4}$] | B. | [-1,-$\frac{3}{4}$)∪($\frac{3}{4}$,1] | C. | ($\frac{3}{5}$,$\frac{3}{4}$] | D. | [-$\frac{3}{4}$,-$\frac{3}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com