
【题目】已知左、右焦点分别为F1(﹣c,0),F2(c,0)的椭圆 ![]() 过点
过点 ![]() ,且椭圆C关于直线x=c对称的图形过坐标原点.
,且椭圆C关于直线x=c对称的图形过坐标原点.
(I)求椭圆C的离心率和标准方程.
(II)圆 ![]() 与椭圆C交于A,B两点,R为线段AB上任一点,直线F1R交椭圆C于P,Q两点,若AB为圆P1的直径,且直线F1R的斜率大于1,求|PF1||QF1|的取值范围.
与椭圆C交于A,B两点,R为线段AB上任一点,直线F1R交椭圆C于P,Q两点,若AB为圆P1的直径,且直线F1R的斜率大于1,求|PF1||QF1|的取值范围.
【答案】解:(Ⅰ)∵椭圆C过点  ,∴
,∴ ![]() ,① ∵椭圆C关于直线x=c对称的图形过坐标原点,∴a=2c,
,① ∵椭圆C关于直线x=c对称的图形过坐标原点,∴a=2c,
∵a2=b2+c2 , ∴ ![]() ,②
,②
由①②得a2=4,b2=3,a=2,c=1,
∴椭圆C的离心率 ![]() ,标准方程为
,标准方程为 ![]() .
.
(Ⅱ)因为AB为圆P1的直径,所以点P1 为线段AB的中点,
为线段AB的中点,
设A(x1 , y1),B(x2 , y2),则, 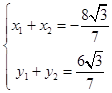 ,又
,又 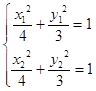 ,
,
所以 ![]() ,则(x1﹣x2)﹣(y1﹣y2)=0,故
,则(x1﹣x2)﹣(y1﹣y2)=0,故 ![]() ,则直线AB的方程为
,则直线AB的方程为 ![]() ,即
,即 ![]() .
.
代入椭圆C的方程并整理得 ![]() ,
,
则 ![]() ,故直线F1R的斜率
,故直线F1R的斜率 ![]() .
.
设F1R:y=k(x+1),由  ,得(3+4k2)x2+8k2x+4k2﹣12=0,
,得(3+4k2)x2+8k2x+4k2﹣12=0,
设P(x3 , y3),Q(x4 , y4),则有 ![]() ,
, ![]() .
.
又 ![]() ,
, ![]() ,
,
所以|PF1||QF1|=(1+k2)|x3x4+(x3+x4)+1|= ![]() ,
,
因为 ![]() ,所以
,所以 ![]() ,
,
即|PF1||QF1|的取值范围是 ![]()
【解析】(Ⅰ)利用椭圆C过点 ![]() ,∵椭圆C关于直线x=c对称的图形过坐标原点,推出a=2c,然后求解椭圆C的离心率,标准方程.(Ⅱ)设A(x1 , y1),B(x2 , y2),利用中点坐标公式以及平方差法求出AB的斜率,得到直线AB的方程,代入椭圆C的方程求出点的坐标,设F1R:y=k(x+1),联立
,∵椭圆C关于直线x=c对称的图形过坐标原点,推出a=2c,然后求解椭圆C的离心率,标准方程.(Ⅱ)设A(x1 , y1),B(x2 , y2),利用中点坐标公式以及平方差法求出AB的斜率,得到直线AB的方程,代入椭圆C的方程求出点的坐标,设F1R:y=k(x+1),联立 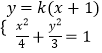 ,设P(x3 , y3),Q(x4 , y4),利用韦达定理,结合
,设P(x3 , y3),Q(x4 , y4),利用韦达定理,结合 ![]() ,
, ![]() ,化简|PF1||QF1|,通过
,化简|PF1||QF1|,通过 ![]() ,求解|PF1||QF1|的取值范围.
,求解|PF1||QF1|的取值范围.


 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且对任意正整数n都有an= ![]() Sn+2成立.若bn=log2an , 则b1008=( )
Sn+2成立.若bn=log2an , 则b1008=( )
A.2017
B.2016
C.2015
D.2014
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬传统文化,某校举行诗词大赛.经过层层选拔,最终甲乙两人进入决赛,争夺冠亚军.决赛规则如下:①比赛共设有五道题;②比赛前两人答题的先后顺序通过抽签决定后,双方轮流答题,每次回答一道,;③若答对,自己得1分;若答错,则对方得1分;④先得 3 分者获胜.已知甲、乙答对每道题的概率分别为 ![]() 和
和 ![]() ,且每次答题的结果相互独立.
,且每次答题的结果相互独立.
(Ⅰ)若乙先答题,求甲3:0获胜的概率;
(Ⅱ)若甲先答题,记乙所得分数为 X,求X的分布列和数学期望 EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列{an}是公差为2的等差数列,数列{bn}满足b1=1,b2=2,且anbn+bn=nbn+1 .
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)设数列{cn}满足cn= ![]() ,数列{cn}的前n项和为Tn , 若不等式(﹣1)nλ<Tn+
,数列{cn}的前n项和为Tn , 若不等式(﹣1)nλ<Tn+ ![]() 对一切n∈N* , 求实数λ的取值范围.
对一切n∈N* , 求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=1+x﹣ ![]() ,g (x)=1﹣x+
,g (x)=1﹣x+ ![]() ,设函数F(x)=f(x﹣4)g(x+3),且函数 F ( x) 的零点均在区间[a,b]( a<b,a,b∈Z )内,则 b﹣a 的最小值为 .
,设函数F(x)=f(x﹣4)g(x+3),且函数 F ( x) 的零点均在区间[a,b]( a<b,a,b∈Z )内,则 b﹣a 的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.命题p:“ ![]() ”,则?p是真命题
”,则?p是真命题
B.命题“?x∈R使得x2+2x+3<0”的否定是:“?x∈R,x2+2x+3>0”
C.“x=﹣1”是“x2+2x+3=0”的必要不充分条件
D.“a>1”是“f(x)=logax(a>0,a≠1)在(0,+∞)上为增函数”的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sinx,﹣1),
=(sinx,﹣1), ![]() =(
=( ![]() cosx,﹣
cosx,﹣ ![]() ),函数f(x)=(
),函数f(x)=( ![]() )
) ![]() ﹣2.
﹣2.
(1)求函数f(x)的最小正周期T;
(2)已知a,b,c分别为△ABC内角A,B,C的对边,其中A为锐角,a=2 ![]() ,c=4,且f(A)=1,求A,b和△ABC的面积S.
,c=4,且f(A)=1,求A,b和△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(x﹣1)+ax2+x+1,g(x)=(x﹣1)ex+ax2 , a∈R. (Ⅰ)当a=1时,求函数f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若函数g(x)有两个零点,试求a的取值范围;
(Ⅲ)证明f(x)≤g(x)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com