Question

【题目】已知某市2015年全年空气质量等级如表1所示.

表1

空气质量等级（空气质量指数（AQI））	频数	频率
优（）	83	22.8%
良（）	121	33.2%
轻度污染（）	68	18.6%
中度污染（）	49	13.4%
重度污染（）	30	8.2%
严重污染（）	14	3.8%
合计	365	100%

2016年5月和6月的空气质量指数如下：

5月 240 80 56 53 92 126 45 87 56 60

191 62 55 58 56 53 89 90 125 124

103 81 89 44 34 53 79 81 62 116

88

6月 63 92 110 122 102 116 81 163 158 76

33 102 65 53 38 55 52 76 99 127

120 80 108 33 35 73 82 90 146 95

选择合适的统计图描述数据，并回答下列问题：

（1）分析该市2016年6月的空气质量情况.

（2）比较该市2016年5月和6月的空气质量，哪个月的空气质量较好？

（3）比较该市2016年6月与该市2015年全年的空气质量，2016年6月的空气质量是否好于去年？

Answer 1

【答案】（1）见解析；（2）5月的空气质量略好于6月，但5月有重度污染，而6月没有；（3）2016年6月的空气质量要好于2015年全年的空气质量.

【解析】

（1）根据该市2016年6月的空气质量指数和空气质量等级分级标准，画出该市这个月的不同空气质量等级的频数与频率分布表；

（2）根据该市2016年5月的空气质量指数和空气质量分级标准，可以画出该市这个月的不同空气质量等级的频数和频率分布表，再与6月份进行比较；

（3）把2016年6月和2015年全年的空气质量进行比较，由于一个月和一年的天数差别很大，所以直接通过频数比较没有意义，应该转化成频率分布进行比较.可以通过二者的空气质量指数的频率分布直方图或空气质量等级的频率分布条形图进行比较.

（1）根据该市2016年6月的空气质量指数和空气质量等级分级标准，可以画出该市这个月的不同空气质量等级的频数与频率分布表（表2）.

表2

	空气质量等级						合计
	优	良	轻度污染	中度污染	重度污染	严重污染
天数	4	15	9	2	0	0	30
比例	13.33%	50%	30%	6.67%	0	0	100%

从表中可以看出，“优”“良”的天数达19天，占了整月的63.33%，没有出现“重度污染”和“严重污染”.

我们可以用条形图和扇形图对数据作出直观的描述，如图1和图2.从条形图中可以看出，在前三个等级的占绝大多数，空气质量等级为“良”的天数最多，后三个等级的天数很少.从扇形图中可以看出，空气质量为“良”的天数占了总天数的一半，大约有三分之二为“优”“良”，大多数是“良”和“轻度污染”.因此，整体上6月的空气质量不错.

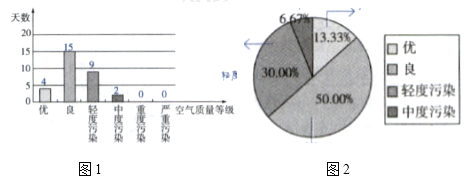
我们还可以用折线图展示空气质量指数随时间的变化情况，如图3.容易发现，6月的空气质量指数在100附近波动.

（2）根据该市2016年5月的空气质量指数和空气质量分级标准，可以画出该市这个月的不同空气质量等级的频数和频率分布表（表3）.

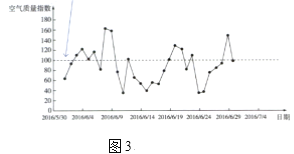
表3

	空气质量等级						合计
	优	良	轻度污染	中度污染	重度污染	严重污染
天数	3	21	5	1	1	0	31
比例	10%	68%	10%	3%	3%	0	100%

为了便于比较，我们选用复合条形图，将两组数据同时反映到一个条形图上.通过条形图中柱的高低，可以更真观地进行两个月的空气质量的比较（图4）.

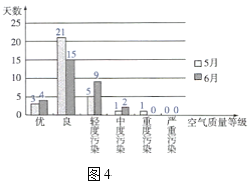
由表3和图4可以发现，5月空气质量为“优”和“良”的总天数比6月多.所以，从整体上看，5月的空气质量略好于6月，但5月有重度污染，而6月没有.

（3）把2016年6月和2015年全年的空气质量进行比较，由于一个月和一年的天数差别很大，所以直接通过频数比较没有意义，应该转化成频率分布进行比较.可以通过二者的空气质量指数的频率分布直方图或空气质量等级的频率分布条形图进行比较（图5）.

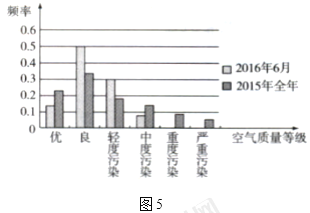
通过图5可以看出，虽然2016年6月的空气质量为“优”的频率略低于2015年，但“良”的频率明显高于2015年，而且2016年6月中度以上的污染天气频率明显小于2015年.所以从整体上看，2016年6月的空气质量要好于2015年全年的空气质量.