
【题目】已知函数f(x)=x|x﹣a|的定义域为D,其中a为常数;
(1)若D=R,且f(x)是奇函数,求a的值;
(2)若a≤﹣1,D=[﹣1,0],函数f(x)的最小值是g(a),求g(a)的最大值;
(3)若a>0,在[0,3]上存在n个点xi(i=1,2,…,n,n≥3),满足x1=0,xn=3,x1<x2<…<xn , 使|f(x1)﹣f(x2)|+|f(x2)﹣f(x3)|+…+|f(xn﹣1)﹣f(xn)|= ![]() ,求实数a的取值.
,求实数a的取值.
【答案】
(1)解:∵f(x)是R上的奇函数,
∴f(﹣1)+f(1)=﹣|﹣1﹣a|+|1﹣a|=0,
∴|a﹣1|=|a+1|,解得a=0.
∴f(x)=x|x|,经过验证满足题意
(2)解:a≤﹣1,D=[﹣1,0],函数f(x)=x(x﹣a)= ![]() ﹣
﹣ ![]() ,
,
①a≤﹣2时,对称轴x= ![]() ≤﹣1,函数f(x)在D上单调递增,
≤﹣1,函数f(x)在D上单调递增,
∴f(x)的最小值是f(﹣1)=﹣(﹣1﹣a)=a+1,
则g(a)≤﹣2+1=﹣1,
故g(a)的最大值为﹣1;
②﹣2<a≤﹣1时,对称轴x= ![]() ∈
∈ ![]() ,函数f(x)在(
,函数f(x)在( ![]() ,﹣
,﹣ ![]() )上单调递增,
)上单调递增,
在[﹣1, ![]() ]单调递减;
]单调递减;
∴f(x)的最小值是f( ![]() )=﹣
)=﹣ ![]() ,
,
则g(a)≤﹣ ![]() ,
,
故g(a)的最大值为﹣ ![]()
(3)解:a>0,函数f(x)=x|x﹣a|的图象可由f(x)=x|x|的图象右移a个单位得到.
而f(x)=x|x|= 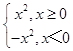 ,x>0时递增,x<0时递增,且f(x)的图象连续,
,x>0时递增,x<0时递增,且f(x)的图象连续,
则函数f(x)=x|x﹣a|在[0,3]递增,
即有|f(x1)﹣f(x2)|+|f(x2)﹣f(x3)|+…+|f(xn﹣1)﹣f(xn)|= ![]() ,
,
化为﹣(f(x1)﹣f(x2)+f(x2)﹣f(x3)+…+f(xn﹣1)﹣f(xn))= ![]() ,
,
即﹣(f(0)﹣f(3))= ![]() ,
,
则3|3﹣a|﹣0= ![]() ,
,
解得a= ![]() 或
或 ![]() .
.
则实数a的取值为{ ![]() ,
, ![]() }
}
【解析】(1)由奇函数的定义可得f(﹣1)+f(1)=0,解得a=0,即可得到f(x)的解析式;(2)化简f(x),对a讨论,①a≤﹣2时,②﹣2<a≤﹣1时,由二次函数对称轴,结合单调性即可得到最值;(3)a>0,函数f(x)=x|x﹣a|的图象可由f(x)=x|x|的图象右移a个单位得到.判断f(x)=x|x|在R上递增,可得函数f(x)=x|x﹣a|在[0,3]递增,去掉绝对值,化简整理计算即可得到a的取值.
【考点精析】解答此题的关键在于理解函数的最值及其几何意义的相关知识,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值,以及对函数的奇偶性的理解,了解偶函数的图象关于y轴对称;奇函数的图象关于原点对称.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且3cosBcosC+1=3sinBsinC+cos2A.
(1)求角A的大小;
(2)若 ![]() ,求b+c的最大值.
,求b+c的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在(﹣4,4)上的奇函数,满足f(2)=1,当﹣4<x≤0时,有f(x)=![]() .
.
(1)求实数a,b的值;
(2)若f(m+1)+![]() >0.求m的取值范围.
>0.求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣mx(m∈R).
(1)若曲线y=f(x)过点P(1,﹣1),求曲线y=f(x)在点P处的切线方程;
(2)求函数f(x)在区间[1,e]上的最大值;
(3)若函数f(x)有两个不同的零点x1 , x2 , 求证:x1x2>e2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为1的半圆O与等边三角形ABC夹在两平行线l1 , l2之间,l∥l1 , l与半圆相交于F,G两点,与三角形ABC两边相交于E,D两点.设弧 ![]() 的长为x(0<x<π),y=EB+BC+CD,若l从l1平行移动到l2 , 则函数y=f(x)的图象大致是( )
的长为x(0<x<π),y=EB+BC+CD,若l从l1平行移动到l2 , 则函数y=f(x)的图象大致是( ) 
A.
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AC 是圆 O 的直径,点 B 在圆 O 上,∠BAC=30°,BM⊥AC交 AC 于点 M,EA⊥平面ABC,FC//EA,AC=4,EA=3,FC=1.
(1)证明:EM⊥BF;
(2)求平面 BEF 与平面ABC 所成的二面角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点列An(an , bn)(n∈N*)均为函数y=ax(a>0,a≠1)的图象上,点列Bn(n,0)满足|AnBn|=|AnBn+1|,若数列{bn}中任意连续三项能构成三角形的三边,则a的取值范围为( )
A.(0, ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
B.( ![]() ,1)∪(1,
,1)∪(1, ![]() )
)
C.(0, ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
D.( ![]() ,1)∪(1,
,1)∪(1, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗,2018年春节前夕,![]() 市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.

(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)①由直方图可以认为,速冻水饺的该项质量指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在
落在![]() 内的概率;
内的概率;
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于![]() 内的包数为
内的包数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com