
设函数 ,
,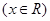 的图象关于直线
的图象关于直线 对称,其中
对称,其中 为常数,且
为常数,且 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)若 的图象经过点
的图象经过点 ,求函数
,求函数 在
在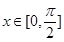 上的值域.
上的值域.
(1)最小正周期是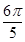 ; (2) [-1-
; (2) [-1-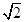 ,2-
,2-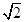 ].
].
【解析】
试题分析:(1) 利用倍角公式将函数化为一角一函数形式,根据正弦函数的图象和性质求解;(2)求出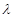 ,将函数具体化,然后利用正弦函数的特征解答.
,将函数具体化,然后利用正弦函数的特征解答.
试题解析:(1)因为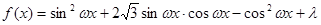 =-cos 2ωx+
=-cos 2ωx+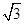 sin 2ωx+λ=2sin (2ωx-
sin 2ωx+λ=2sin (2ωx-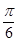 )+λ,
)+λ,
由直线x=π是y=f(x)图象的一条对称轴,可得
sin (2ωπ-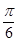 )=±1,
)=±1,
所以2ωπ-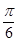 =kπ+
=kπ+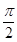 (k∈Z),即ω=
(k∈Z),即ω=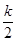 +
+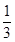 (k∈Z).
(k∈Z).
又ω∈(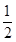 ,1),k∈Z,所以k=1,故ω=
,1),k∈Z,所以k=1,故ω=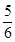 .
.
所以f(x)的最小正周期是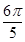 .
.
(2)由y=f(x)的图象过点(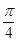 ,0),得f(
,0),得f(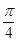 )=0,
)=0,
即λ=-2sin (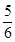 ×
×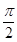 -
-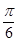 )=-2sin
)=-2sin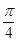 =-
=-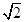 ,
,
即λ=-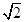 .
.
故f(x)=2sin (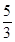 x-
x-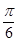 )-
)-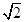 ,
,
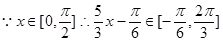 函数f(x)的值域为[-1-
函数f(x)的值域为[-1-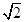 ,2-
,2-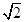 ].
].
考点:倍角公式、正弦函数的图象和性质、函数值域.


科目:高中数学 来源:2012-2013学年山东省威海市乳山一中高三(上)12月月考数学试卷(文科)(解析版) 题型:解答题
 ,
, ,设函数
,设函数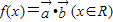 的图象关于直线
的图象关于直线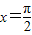 对称,其中ω为常数,且ω∈(0,1).
对称,其中ω为常数,且ω∈(0,1). ,再将所得图象向右平移
,再将所得图象向右平移 个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在区间
个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在区间 上有且只有一个实数解,求实数k的取值范围.
上有且只有一个实数解,求实数k的取值范围.查看答案和解析>>
科目:高中数学 来源:2013年广东省高考数学最后模拟试卷(理科)(解析版) 题型:选择题
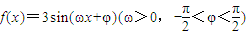 的图象关于直线x=
的图象关于直线x=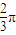 对称,它的周期是π,则( )
对称,它的周期是π,则( ) )
)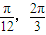 ]上是减函数
]上是减函数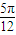 ,0)
,0)查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省宁波市金兰合作组织高三上学期期中联考文科数学试卷(解析版) 题型:解答题
(本题14分)已知向量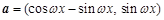 ,
,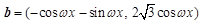 ,设函数
,设函数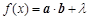
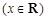 的图象关于直线
的图象关于直线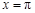 对称,其中
对称,其中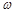 ,
,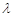 为常数,且
为常数,且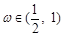 .
.
(Ⅰ)求函数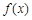 的最小正周期;
的最小正周期;
(Ⅱ)若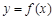 的图象经过点
的图象经过点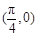 ,求函数
,求函数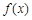 在区间
在区间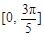 上的取值范围.
上的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com