
【题目】已知![]() 是定义在
是定义在![]() 上的函数,记
上的函数,记![]() ,
,![]() 的最大值为
的最大值为![]() .若存在
.若存在![]() ,满足
,满足![]()
![]()
![]() ,则称一次函数
,则称一次函数![]() 是
是![]() 的“逼近函数”,此时的
的“逼近函数”,此时的![]() 称为
称为![]() 在
在![]() 上的“逼近确界”.
上的“逼近确界”.
(1)验证:![]() 是
是![]()
![]() 的“逼近函数”;
的“逼近函数”;
(2)已知![]()
![]()
![]()
![]() .若
.若![]() 是
是![]() 的“逼近函数”,求
的“逼近函数”,求![]() 的值;
的值;
(3)已知![]()
![]() 的逼近确界为
的逼近确界为![]() ,求证:对任意常数
,求证:对任意常数![]() ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=![]() 若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”近年来成为了百姓耳熟能详的热门词汇,对于旅游业来说,“一带一路”战略的提出,让“丝路之旅”超越了旅游产品、旅游线路的简单范畴,赋予了旅游促进跨区域融合的新理念. 而其带来的设施互通、经济合作、人员往来、文化交融更是将为相关区域旅游发展带来巨大的发展机遇.为此,旅游企业们积极拓展相关线路;各地旅游主管部门也在大力打造丝路特色旅游品牌和服务.某市旅游局为了解游客的情况,以便制定相应的策略. 在某月中随机抽取甲、乙两个景点10天的游客数,统计得到茎叶图如下:

(1)若将图中景点甲中的数据作为该景点较长一段时期内的样本数据,以每天游客人数频率作为概率.今从这段时期内任取4天,记其中游客数超过130人的天数为![]() ,求概率
,求概率![]() ;
;
(2)现从上图20天的数据中任取2天的数据(甲、乙两景点中各取1天),记其中游客数不低于125且不高于135人的天数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,…,
,…,![]() 是由
是由![]() (
(![]() )个整数
)个整数![]() ,
,![]() ,…,
,…,![]() 按任意次序排列而成的数列,数列
按任意次序排列而成的数列,数列![]() 满足
满足![]() (
(![]() ).
).
(1)当![]() 时,写出数列
时,写出数列![]() 和
和![]() ,使得
,使得![]() .
.
(2)证明:当![]() 为正偶数时,不存在满足
为正偶数时,不存在满足![]() (
(![]() )的数列
)的数列![]() .
.
(3)若![]() ,
,![]() ,…,
,…,![]() 是
是![]() ,
,![]() ,…,
,…,![]() 按从大到小的顺序排列而成的数列,写出
按从大到小的顺序排列而成的数列,写出![]() (
(![]() ),并用含
),并用含![]() 的式子表示
的式子表示![]() .
.
(参考:![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,直线
,直线![]() 和
和![]() 相交于点
相交于点![]() ,且
,且![]() 和
和![]() 的斜率之差是1.
的斜率之差是1.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过轨迹![]() 上的点
上的点![]() ,
,![]() ,作圆
,作圆![]() :
:![]() 的两条切线,分别交
的两条切线,分别交![]() 轴于点
轴于点![]() ,
,![]() .当
.当![]() 的面积最小时,求
的面积最小时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知菱形![]() 中,
中,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,将
,将![]() 沿
沿![]() 折起,使顶点
折起,使顶点![]() 至点
至点![]() ,在折起的过程中,下列结论正确的是( )
,在折起的过程中,下列结论正确的是( )
A.![]() B.存在一个位置,使
B.存在一个位置,使![]() 为等边三角形
为等边三角形
C.![]() 与
与![]() 不可能垂直D.直线
不可能垂直D.直线![]() 与平面
与平面![]() 所成的角的最大值为
所成的角的最大值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() )与双曲线
)与双曲线![]() (
(![]() ,
,![]() )有相同的焦点
)有相同的焦点![]() ,点
,点![]() 是两条曲线的一个交点,且
是两条曲线的一个交点,且![]() 轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是( )
轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程
的参数方程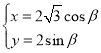 (
(![]() 为参数).直线
为参数).直线![]() 的参数方程
的参数方程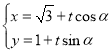 (
(![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 在直角坐标系中的普通方程;
在直角坐标系中的普通方程;
(Ⅱ)以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,当曲线
轴的正半轴为极轴建立极坐标系,当曲线![]() 截直线
截直线![]() 所得线段的中点极坐标为
所得线段的中点极坐标为![]() 时,求直线
时,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有次水下考古活动中,潜水员需潜入水深为30米的水底进行作业,其用氧量包含以下三个方面:①下潜时,平均速度为每分钟![]() 米,每分钟的用氧量为
米,每分钟的用氧量为![]() 升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟
升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟![]() 米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为
米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为![]() 升;
升;
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)若![]() ,求总用氧量
,求总用氧量![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com