
����Ŀ����ɫ����Խ��Խ�ܵ����Ĺ�ע��Խ��Խ��������߶�����Դ��������Ȥ![]() ���������߱ȽϹ��ĵ���������������ʻ���
���������߱ȽϹ��ĵ���������������ʻ���![]() ij�о�С��������г��������ȡ20�����綯������������ʻ���
ij�о�С��������г��������ȡ20�����綯������������ʻ���![]() ���γ�������ʻ��������
���γ�������ʻ��������![]() ����������������ʻ���ȫ������50�����300����֮�䣬��ͳ�ƽ���ֳ�5�飺
����������������ʻ���ȫ������50�����300����֮�䣬��ͳ�ƽ���ֳ�5�飺 ![]() �����Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
�����Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
![]() ��ֱ��ͼ��m��ֵ��
��ֱ��ͼ��m��ֵ��
![]() �ε�������ʻ�����
�ε�������ʻ�����![]() �ij�������
�ij�������
![]() ������ʻ�����
������ʻ�����![]() �ij����������ȡ2������������ǡ��һ������ʻ�����
�ij����������ȡ2������������ǡ��һ������ʻ�����![]() �ĸ��ʣ�
�ĸ��ʣ�

���𰸡�![]() .
.
����������������� ![]() ����С���ε������Ϊ1�����mֵ��
����С���ε������Ϊ1�����mֵ��
![]() �����ʻ�����
�����ʻ�����![]() �ij�����Ƶ�ʣ�������Ƶ��
�ij�����Ƶ�ʣ�������Ƶ��![]() Ƶ��
Ƶ��![]() ����������������
����������������
![]() ����������ϣ��ֱ����5���������ȡ2�����ij鷨����������ǡ��һ����������ʻ���Ϊ
����������ϣ��ֱ����5���������ȡ2�����ij鷨����������ǡ��һ����������ʻ���Ϊ![]() �鷨���������ݹŵ���͵ĸ��ʹ�ʽ���㣮
�鷨���������ݹŵ���͵ĸ��ʹ�ʽ���㣮
���������
![]() ��ֱ��ͼ�ɵã�
��ֱ��ͼ�ɵã� ![]() ��
��![]()
![]() ������֪��ʻ�����
������֪��ʻ�����![]() �ij�����Ϊ
�ij�����Ϊ![]()
![]() ������֪����ʻ�����
������֪����ʻ�����![]() �ij�����Ϊ3����Ϊ
�ij�����Ϊ3����Ϊ![]() ��
��
��ʻ�����![]() �ij�����Ϊ2����Ϊ
�ij�����Ϊ2����Ϊ![]() ��
��
����10�������¼��� ![]() ��
��
�衰����ǡ��һ������ʻ�����![]() ��Ϊ�¼�A��
��Ϊ�¼�A��
���¼�A����6�������¼��� ![]() ��
��
��![]() .
.


 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4��4������ϵ���������
��ƽ��ֱ������ϵ�У�ԲC�ķ���Ϊ (��Ϊ����).������ԭ��OΪ���㣬
(��Ϊ����).������ԭ��OΪ���㣬 ![]() ���������Ϊ���ᣬ����������ϵ����������ϵ��ȡ��ͬ�ĵ�λ���ȣ�ֱ��
���������Ϊ���ᣬ����������ϵ����������ϵ��ȡ��ͬ�ĵ�λ���ȣ�ֱ��![]() �ļ����귽��
�ļ����귽��![]() .
.
(��)��![]() ʱ���ж�ֱ��
ʱ���ж�ֱ��![]() ��
��![]() �Ĺ�ϵ��
�Ĺ�ϵ��
(��)��![]() ������ֻ��һ�㵽ֱ��
������ֻ��һ�㵽ֱ��![]() �ľ������
�ľ������![]() ʱ����
ʱ����![]() �ϵ�ֱ��
�ϵ�ֱ��![]() ����Ϊ
����Ϊ![]() �ĵ������.
�ĵ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC���ڽ�A��B��C���Եı�a��b��c���� ![]()
��1�����A
��2���� ![]() ����a����Сֵ��
����a����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������У���1��ʼ���ΰ����¹���ȡ�������һ��ȡ1���ڶ���ȡ2������ż��2��4��������ȡ3����������5��7��9�����Ĵ�ȡ4������ż��10��12��14��16�������ȡ5����������17��19��21��23��25�����˹���ȡ��ȥ���õ�һ��������1��2��4��5��7��9��10��12��14��16��17��19����������������е�2014�����ǣ� ��
A. 3965 B. 3966 C. 3968 D. 3989
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ABCD�������Σ�O�������ε����ģ�PO�͵���ABCD������߳�Ϊa��E��PC���е㣮
������֤��PA��ƽ��BDE��
����ƽ��PAC��ƽ��BDE��
�����������E-BD-CΪ30�㣬������P-ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��B��C�ǵ�λԲ������������ͬ�ĵ㣮�� ![]() ����
���� ![]() ����Сֵ�ǣ� ��
����Сֵ�ǣ� ��
A.0
B.- ![]()
C.- ![]()
D.- ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڹ���Ϊ2�ĵȱ�����{an}�У�a2��a3�ĵȲ�������9 ![]() ��
��
��1����a1��ֵ��
��2��������y=|a1|sin�� ![]() x+�գ���|��|���У���һ����ͼ����ͼ��ʾ��M����1��|a1|����N��3����|a1|��Ϊͼ���ϵ����㣬���MPN=�£�����P������ԭ��O�غϣ�0���£��У���tan���թ��£���ֵ��
x+�գ���|��|���У���һ����ͼ����ͼ��ʾ��M����1��|a1|����N��3����|a1|��Ϊͼ���ϵ����㣬���MPN=�£�����P������ԭ��O�غϣ�0���£��У���tan���թ��£���ֵ�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ex��x2��ax��
��1��������y=f��x���ڵ�x=0��������б��Ϊ1������f��x����[0��1]�ϵ���ֵ��
��2����g��x��=f��x��+ ![]() ��x2��a2������x��0ʱ��g��x����0���������ʵ��a��ȡֵ��Χ��
��x2��a2������x��0ʱ��g��x����0���������ʵ��a��ȡֵ��Χ��
��3����a=0��x��0ʱ��֤��f��x����ex��xlnx��x2��x+1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
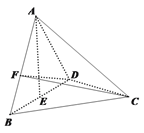
����Ŀ����ͼ��������![]() �У���֪
�У���֪![]() ���DZ߳�Ϊ
���DZ߳�Ϊ![]() �ĵȱ������Σ�
�ĵȱ������Σ�![]() Ϊ
Ϊ![]() �е㣬��
�е㣬��![]() ƽ��
ƽ��![]() ��
��![]() Ϊ�߶�
Ϊ�߶�![]() ��һ���㣬��
��һ���㣬��![]() ��
��
��1����![]() ʱ��������ֱ��
ʱ��������ֱ��![]() ��
��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
��2����![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵΪ
���ɽǵ�����ֵΪ![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com