
【题目】在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() :
:![]() ,直线
,直线![]() :
:![]() .
.
(1)求曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+![]() ,且此函数的图象过点(1,5).
,且此函数的图象过点(1,5).
(1)求实数m的值并判断f(x)的奇偶性;
(2)判断函数f(x)在[2,+∞)上的单调性,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部门为了解人们对“延迟退休年龄政策”的支持度,随机调查了![]() 人,其中男性
人,其中男性![]() 人.调查发现持不支持态度的有
人.调查发现持不支持态度的有![]() 人,其中男性占
人,其中男性占![]() .分析这
.分析这![]() 个持不支持态度的样本的年龄和性别结构,绘制等高条形图如图所示.
个持不支持态度的样本的年龄和性别结构,绘制等高条形图如图所示.
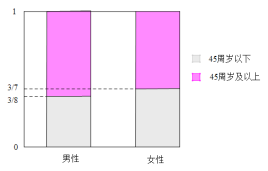
(1)在持不支持态度的人中,![]() 周岁及以上的男女比例是多少?
周岁及以上的男女比例是多少?
(2)调查数据显示,![]() 个持支持态度的人中有
个持支持态度的人中有![]() 人年龄在
人年龄在![]() 周岁以下.填写下面的
周岁以下.填写下面的![]() 列联表,问能否有
列联表,问能否有![]() 的把握认为年龄是否在
的把握认为年龄是否在![]() 周岁以下与对“延迟退休年龄政策”的态度有关.
周岁以下与对“延迟退休年龄政策”的态度有关.

参考公式及数据: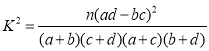 ,
,![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设三棱锥![]() 的底面是正三角形,侧棱长均相等,
的底面是正三角形,侧棱长均相等,![]() 是棱
是棱![]() 上的点(不含端点),记直线
上的点(不含端点),记直线![]() 与直线
与直线![]() 所成角为
所成角为![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,二面角
,二面角![]() 的平面角为
的平面角为![]() ,则( )
,则( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校通过自主招生方式在贵阳招收一名优秀的高三毕业生,经过层层筛选,甲、乙两名学生进入最后测试,该校设计了一个测试方案:甲、乙两名学生各自从6个问题中随机抽3个问题.已知这6道问题中,学生甲能正确回答其中的4个问题,而学生乙能正确回答每个问题的概率均为![]() ,甲、乙两名学生对每个问题的回答都是相互独立、互不影响的.
,甲、乙两名学生对每个问题的回答都是相互独立、互不影响的.
(1)求甲、乙两名学生共答对2个问题的概率.
(2)请从期望和方差的角度分析,甲、乙两名学生哪位被录取的可能性更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实常数).
为实常数).

(1)当![]() 时,作出
时,作出![]() 的图象,并写出它的单调递增区间;
的图象,并写出它的单调递增区间;
(2)设![]() 在区间
在区间![]() 的最小值为
的最小值为![]() ,求
,求![]() 的表达式;
的表达式;
(3)已知函数![]() 在
在![]() 的情况下:其在区间
的情况下:其在区间![]() 单调递减,在区间
单调递减,在区间![]() 单调递增.设
单调递增.设![]() ,若函数
,若函数![]() 在区间
在区间![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①对于独立性检验,![]() 的值越大,说明两事件相关程度越大;②以模型
的值越大,说明两事件相关程度越大;②以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() ,
,![]() 的值分别是
的值分别是![]() 和
和![]() ;③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程
;③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() ;④通过回归直线
;④通过回归直线![]() 及回归系数
及回归系数![]() ,可以精确反映变量的取值和变化趋势,其中正确的个数是( )
,可以精确反映变量的取值和变化趋势,其中正确的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com