
【题目】如图,椭圆![]()
![]() 的离心率是
的离心率是![]() ,左右焦点分别为
,左右焦点分别为![]() ,
,![]() ,过点
,过点![]() 的动直线
的动直线![]() 与椭圆相交于
与椭圆相交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 过
过![]() 时,
时,![]() 的周长为
的周长为![]() .
.
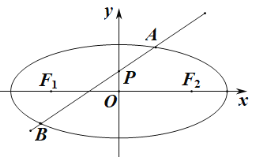
(1)求椭圆![]() 的方程;
的方程;
(2)当![]() 时,求直线
时,求直线![]() 方程;
方程;
(3)已知点![]() ,直线
,直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .问是否存在实数
.问是否存在实数![]() ,使得
,使得![]() 恒成立?
恒成立?
【答案】(1) ![]() (2)
(2) ![]() (3)存在,
(3)存在,![]()
【解析】
(1)由焦点三角形的周长特点可求出![]() 值,再结合椭圆离心率是
值,再结合椭圆离心率是![]() ,可求出
,可求出![]() ,进而求得椭圆标准方程;
,进而求得椭圆标准方程;
(2),设直线方程为![]() ,
,![]() ,
,![]() ,可联立直线方程和椭圆标准方程,得出两根和与积的表达式,再结合
,可联立直线方程和椭圆标准方程,得出两根和与积的表达式,再结合![]() ,代换出
,代换出![]() 与
与![]() 的关系式;
的关系式;
(3)先用必要性探路,找特殊情况,当![]() 轴可知
轴可知![]() ,此时存在
,此时存在![]() 使得
使得![]() 成立,根据题意和斜率定义表示出
成立,根据题意和斜率定义表示出![]() ,结合(2)中韦达定理即可得证
,结合(2)中韦达定理即可得证
(1)由椭圆定义知![]() 的周长为
的周长为![]() ,
,
所以![]() ,所以
,所以![]()
又离心率![]() ,所以
,所以![]() ,所以
,所以![]()
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)当![]() 轴,
轴,![]()
所以可设![]() ,
,![]() ,
,![]()
则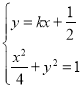 ,消去
,消去![]() 得
得![]()
所以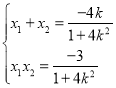
![]()
因为![]() ,
,
所以![]() ,即
,即![]() 代入
代入![]() 化简得
化简得
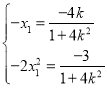 所以
所以![]()
解得![]()
所以直线![]() 方程为:
方程为:![]() ,
,
(3)当![]() 轴可知
轴可知![]() ,此时存在
,此时存在![]() 使得
使得![]() 成立,
成立,
下面证明当![]() 时
时![]() 恒成立
恒成立

因为![]()
所以![]() 恒成立
恒成立
即存在![]() ,使得
,使得![]() 恒成立.
恒成立.


科目:高中数学 来源: 题型:
【题目】若数列![]() 的每一项都不等于零,且对于任意的
的每一项都不等于零,且对于任意的![]() ,都有
,都有![]() (
(![]() 为常数),则称数列
为常数),则称数列![]() 为“类等比数列”;已知数列
为“类等比数列”;已知数列![]() 满足:
满足:![]()
![]() ,对于任意的
,对于任意的![]() ,都有
,都有![]() ;
;
(1)求证:数列![]() 是“类等比数列”;
是“类等比数列”;
(2)若![]() 是单调递减数列,求实数
是单调递减数列,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,求数列
,求数列![]() 的前
的前![]() 项之积取最大值时
项之积取最大值时![]() 的值;
的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某产品的销售额![]() 与广告费用
与广告费用![]() 之间的关系如下表:
之间的关系如下表:
| 0 | 1 | 2 | 3 | 4 |
| 10 | 15 |
| 30 | 35 |
若根据表中的数据用最小二乘法求得![]() 对
对![]() 的回归直线方程为
的回归直线方程为![]() ,则下列说法中错误的是( )
,则下列说法中错误的是( )
A.产品的销售额与广告费用成正相关
B.该回归直线过点![]()
C.当广告费用为10万元时,销售额一定为74万元
D.![]() 的值是20
的值是20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某款冰淇淋的包装盒为圆台,盒盖为直径为![]() 的圆形纸片,每盒冰淇淋中包含有香草口味、巧克力口味和草莓口味冰淇淋球各一个,假定每个冰淇淋球都是半径为
的圆形纸片,每盒冰淇淋中包含有香草口味、巧克力口味和草莓口味冰淇淋球各一个,假定每个冰淇淋球都是半径为![]() 的球体,三个冰淇淋球两两相切,且都与冰淇淋盒盖、盒底和盒子侧面的曲面相切,则冰淇淋盒的体积为______.
的球体,三个冰淇淋球两两相切,且都与冰淇淋盒盖、盒底和盒子侧面的曲面相切,则冰淇淋盒的体积为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市《城市总体规划(![]() 年)》提出到
年)》提出到![]() 年实现“
年实现“![]() 分钟社区生活圈”全覆盖的目标,从教育与文化、医疗与养老、交通与购物、休闲与健身
分钟社区生活圈”全覆盖的目标,从教育与文化、医疗与养老、交通与购物、休闲与健身![]() 个方面构建“
个方面构建“![]() 分钟社区生活圈”指标体系,并依据“
分钟社区生活圈”指标体系,并依据“![]() 分钟社区生活圈”指数高低将小区划分为:优质小区(指数为
分钟社区生活圈”指数高低将小区划分为:优质小区(指数为![]() )、良好小区(指数为
)、良好小区(指数为![]() )、中等小区(指数为
)、中等小区(指数为![]() )以及待改进小区(指数为
)以及待改进小区(指数为![]() )
)![]() 个等级.下面是三个小区
个等级.下面是三个小区![]() 个方面指标的调查数据:
个方面指标的调查数据:
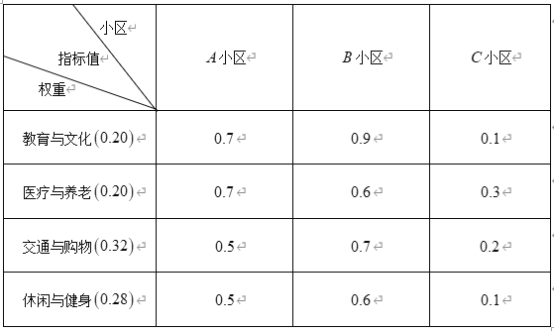
注:每个小区“![]() 分钟社区生活圈”指数
分钟社区生活圈”指数![]() ,其中
,其中![]() 、
、![]() 、
、![]() 、
、![]() 为该小区四个方面的权重,
为该小区四个方面的权重,![]() 、
、![]() 、
、![]() 、
、![]() 为该小区四个方面的指标值(小区每一个方面的指标值为
为该小区四个方面的指标值(小区每一个方面的指标值为![]() 之间的一个数值).
之间的一个数值).
现有![]() 个小区的“
个小区的“![]() 分钟社区生活圈”指数数据,整理得到如下频数分布表:
分钟社区生活圈”指数数据,整理得到如下频数分布表:
分组 |
|
|
|
|
|
频数 |
|
|
|
|
|
(Ⅰ)分别判断![]() 、
、![]() 、
、![]() 三个小区是否是优质小区,并说明理由;
三个小区是否是优质小区,并说明理由;
(Ⅱ)对这![]() 个小区按照优质小区、良好小区、中等小区和待改进小区进行分层抽样,抽取
个小区按照优质小区、良好小区、中等小区和待改进小区进行分层抽样,抽取![]() 个小区进行调查,若在抽取的
个小区进行调查,若在抽取的![]() 个小区中再随机地选取
个小区中再随机地选取![]() 个小区做深入调查,记这
个小区做深入调查,记这![]() 个小区中为优质小区的个数
个小区中为优质小区的个数![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题P:函数![]() 且|f(a)|<2,命题Q:集合A={x|x2+(a+2)x+1=0,x∈R},B={x|x>0}且A∩B=,
且|f(a)|<2,命题Q:集合A={x|x2+(a+2)x+1=0,x∈R},B={x|x>0}且A∩B=,
(1)分别求命题P、Q为真命题时的实数a的取值范围;
(2)当实数a取何范围时,命题P、Q中有且仅有一个为真命题;
(3)设P、Q皆为真时a的取值范围为集合S,![]() ,若RTS,求m的取值范围.
,若RTS,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我们的教材必修一中有这样一个问题,假设你有一笔资金,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报![]() 元;
元;
方案二:第一天回报![]() 元,以后每天比前一天多回报
元,以后每天比前一天多回报![]() 元;
元;
方案三:第一天回报![]() 元,以后每天的回报比前一天翻一番.
元,以后每天的回报比前一天翻一番.
记三种方案第![]() 天的回报分别为
天的回报分别为![]() ,
,![]() ,
,![]() .
.
(1)根据数列的定义判断数列![]() ,
,![]() ,
,![]() 的类型,并据此写出三个数列的通项公式;
的类型,并据此写出三个数列的通项公式;
(2)小王准备做一个为期十天的短期投资,他应该选择哪一种投资方案?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com