
【题目】某地为鼓励群众参与“全民读书活动”,增加参与读书的趣味性.主办方设计这样一个小游戏:参与者抛掷一枚质地均匀的骰子(正方体,六个面上分别标注1,2,3,4,5,6六个数字).若朝上的点数为偶数.则继续抛掷一次.若朝上的点数为奇数,则停止游戏,照这样的规则进行,最多允许抛掷3次.每位参与者只能参加一次游戏.
(1)求游戏结束时朝上点数之和为5的概率;
(2)参与者可以选择两种方案:方案一:游戏结束时,若朝上的点数之和为偶数,奖励3本不同的畅销书;若朝上的点数之和为奇数,奖励1本畅销书.方案二:游戏结束时,最后一次朝上的点数为偶数,奖励5本不同的畅销书,否则,无奖励.试分析哪一种方案能使游戏参与者获得更多畅销书奖励?并说明判断的理由.
【答案】(1)![]() ;(2)选择方案一,理由见解析
;(2)选择方案一,理由见解析
【解析】
(1)游戏结束时朝上点数之和为5的事件为只抛掷1次就结束游戏且朝上点数之和为5、抛掷2次就结束游戏且朝上点数之和为5、掷3次结束游戏且朝上点数之和为5三个互斥事件的和,根据互斥事件的和的概率求解即可;
(2)分别计算方案一、方案二获得畅销书本书的随机变量的期望即可比较方案的优劣.
(1)设事件![]() :只抛掷1次就结束游戏且朝上点数之和为5,事件
:只抛掷1次就结束游戏且朝上点数之和为5,事件![]() :抛掷2次就结束游戏且朝上点数之和为5,事件
:抛掷2次就结束游戏且朝上点数之和为5,事件![]() :掷3次结束游戏且朝上点数之和为5,事件
:掷3次结束游戏且朝上点数之和为5,事件![]() ,
,![]() ,
,![]() 彼此互斥.
彼此互斥.
则![]() ,
,![]() ,
,![]()
游戏结束时朝上点数之和为5,即事件![]() ,其概率为
,其概率为
![]()
(2)方案一:设获得奖励畅销书的本数为![]() ,
,
![]()
![]()
则![]() 的分布列为:
的分布列为:
| 3 | 1 |
|
|
|
![]()
方案二:设获得奖励畅销书的本数为![]()
![]()
![]()
则![]() 的分布列为:
的分布列为:
| 5 | 0 |
|
|
|
![]()
∵![]() ,
,
∴选择方案一能使游戏参与者获得更多畅销书奖励.


科目:高中数学 来源: 题型:
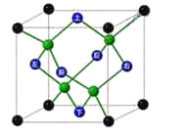
【题目】金刚石是碳原子的一种结构晶体,属于面心立方晶胞(晶胞是构成晶体的最基本的几何单元),即碳原子处在立方体的![]() 个顶点,
个顶点,![]() 个面的中心,此外在立方体的对角线的
个面的中心,此外在立方体的对角线的![]() 处也有
处也有![]() 个碳原子,如图所示(绿色球),碳原子都以共价键结合,原子排列的基本规律是每一个碳原子的周围都有
个碳原子,如图所示(绿色球),碳原子都以共价键结合,原子排列的基本规律是每一个碳原子的周围都有![]() 个按照正四面体分布的碳原子.设金刚石晶胞的棱长为
个按照正四面体分布的碳原子.设金刚石晶胞的棱长为![]() ,则正四面体
,则正四面体![]() 的棱长为__________;正四面体
的棱长为__________;正四面体![]() 的外接球的体积是__________.
的外接球的体积是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线
轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() .若直
.若直![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 网络是一种先进的高频传输技术,我国的
网络是一种先进的高频传输技术,我国的![]() 技术发展迅速,已位居世界前列.华为公司2019年8月初推出了一款
技术发展迅速,已位居世界前列.华为公司2019年8月初推出了一款![]() 手机,现调查得到该款
手机,现调查得到该款![]() 手机上市时间
手机上市时间![]() 和市场占有率
和市场占有率![]() (单位:%)的几组相关对应数据.如图所示的折线图中,横轴1代表2019年8月,2代表2019年9月……,5代表2019年12月,根据数据得出
(单位:%)的几组相关对应数据.如图所示的折线图中,横轴1代表2019年8月,2代表2019年9月……,5代表2019年12月,根据数据得出![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .若用此方程分析并预测该款手机市场占有率的变化趋势,则最早何时该款
.若用此方程分析并预测该款手机市场占有率的变化趋势,则最早何时该款![]() 手机市场占有率能超过0.5%(精确到月)( )
手机市场占有率能超过0.5%(精确到月)( )

A.2020年6月B.2020年7月C.2020年8月D.2020年9月
查看答案和解析>>
科目:高中数学 来源: 题型:
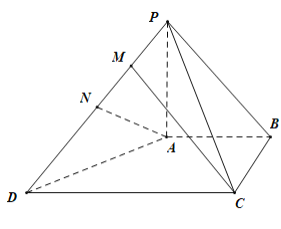
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,N为
,N为![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]()
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值
所成锐二面角的余弦值
(3)在线段![]() 上是否存在一点M,使得直线
上是否存在一点M,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由
的值;若不存在,说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新冠来袭,湖北告急!有一支援鄂医疗小队由3名医生和6名护士组成,他们全部要分配到三家医院.每家医院分到医生1名和护士1至3名,其中护士甲和护士乙必须分到同一家医院,则不同的分配方法有( )种
A.252B.540C.792D.684
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为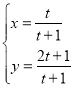 (t为参数),曲线C2的参数方程为
(t为参数),曲线C2的参数方程为![]() (α为参数),以坐标原点为极点.x轴正半轴为极轴建立极坐标系.
(α为参数),以坐标原点为极点.x轴正半轴为极轴建立极坐标系.
(Ⅰ)求曲线C1的普通方程和曲线C2的极坐标方程;
(Ⅱ)射线![]() 与曲线C2交于O,P两点,射线
与曲线C2交于O,P两点,射线![]() 与曲线C1交于点Q,若△OPQ的面积为1,求|OP|的值.
与曲线C1交于点Q,若△OPQ的面积为1,求|OP|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明每天从家步行去学校,有两条路线可以选择,第一条路线,需走天桥,不用等红灯,平均用时910秒;第二条路线,要经过两个红绿灯路口,如图,A处为小明家,D处为学校,走路段![]() 需240秒,在B处有一红绿灯,红灯时长120秒,绿灯时长30秒,走路段
需240秒,在B处有一红绿灯,红灯时长120秒,绿灯时长30秒,走路段![]() 需450秒,在C处也有一红绿灯,红灯时长100秒,绿灯时长50秒,走路段
需450秒,在C处也有一红绿灯,红灯时长100秒,绿灯时长50秒,走路段![]() 需200秒.小明进行了60天的试验,每天都选择第二条路线,并记录了在B处等待红灯的时长,经统计,60天中有48天在B处遇到红灯,根据记录的48天等待红灯时长的数据绘制了下面的频率分布直方图.已知B处和C处的红灯亮起的时刻恰好始终保持相同,且红绿灯之间切换无时间间隔.
需200秒.小明进行了60天的试验,每天都选择第二条路线,并记录了在B处等待红灯的时长,经统计,60天中有48天在B处遇到红灯,根据记录的48天等待红灯时长的数据绘制了下面的频率分布直方图.已知B处和C处的红灯亮起的时刻恰好始终保持相同,且红绿灯之间切换无时间间隔.

(1)若小明选择第二条路线,设当小明到达B处的时刻为B处红灯亮起后的第x秒(![]() )时,小明在B处等待红灯的时长为y秒,求y关于x的函数的解析式;
)时,小明在B处等待红灯的时长为y秒,求y关于x的函数的解析式;
(2)若小明选择第二条路线,请估计小明在B处遇到红灯的概率,并问小明是否可能在B处和C处都遇到红灯;
(3)若取区间中点作为该区间对应的等待红灯的时长,以这两条路线的平均用时作为决策依据,小明应选择哪一条路线?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com