
【题目】如图,已知平面ADC∥平面A1B1C1 , B为线段AD的中点,△ABC≈△A1B1C1 , 四边形ABB1A1为正方形,平面AA1C1C丄平面ADB1A1 , A1C1=A1A,∠C1A1A= ![]() ,M为棱A1C1的中点.
,M为棱A1C1的中点.
(Ⅰ)若N为线段DC1上的点,且直线MN∥平面ADB1A1 , 试确定点N的位置;
(Ⅱ)求平面MAD与平面CC1D所成的锐二面角的余弦值.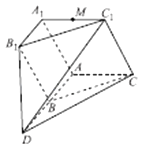
【答案】证明:(Ⅰ)连结A1D,直线MN∥平面ADB1A1 , MN平面A1C′1D, 平面A1C1D∩平面ADB1A1=A1D1 , ∴MN∥A1D,
又M为棱A1C1的中点,∴MN为△A1C1D的中位线,
∴N为DC1的中点.
(Ⅱ)设A1B1=1,则A1A=1,A1C1=1,因为B为AD的中点,所以AD=2,因为△ABC≌△A1B1C1 ,
所以A1C1=AC,又平面ABC∥平面A1B1C1 , 平面A1B1C1∩平面A1AOC1=A1C1 , 平面ABC∩平面A1AOC1=AO,
∴A1C1∥AC,所以四边形A1ACC1是平行四边形,又A1C1=A1A,所以A1ACC1是菱形,又∠C1A1A= ![]() ,
,
A1M= ![]() ,∴
,∴ ![]() ,∴AM⊥A1C1 , ∴AM⊥AC,∵AD⊥AA1 , 平面AA1C1C⊥平面ADB1A1 ,
,∴AM⊥A1C1 , ∴AM⊥AC,∵AD⊥AA1 , 平面AA1C1C⊥平面ADB1A1 ,
∴AD⊥平面AA1C1C,∴AD⊥AM,AD⊥AC,∴AM,AD,AC两两垂直,
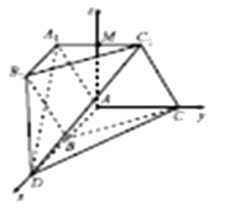
以A为坐标原点,AD,AC,AM分别为x,y,z轴,
由题意可得:A(0,0,0),D(2,0,0),C(0,1,0),C1( ![]() ),∴
),∴ ![]() =(﹣2,1,0),
=(﹣2,1,0), 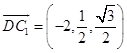 ,
,
设平面CC1D的法向量为: ![]() =(x,y,z),则
=(x,y,z),则 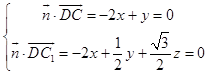 ,
,
令z=2 ![]() ,可得y=6,x=3,可得
,可得y=6,x=3,可得 ![]() =(3,6,2
=(3,6,2 ![]() ),平面MAD的一个法向量为:
),平面MAD的一个法向量为: ![]() =(0,1,0),
=(0,1,0),
平面MAD与平面CC1D所成的锐二面角的余弦值为:cosθ=|cos ![]() |
|
=  =
= ![]() =
= ![]()
【解析】(Ⅰ)连结A1D,直线MN∥平面ADB1A1 , 推出MN∥A1D,说明MN为△A1C1D的中位线,得到N为DC1的中点.(Ⅱ)设A1B1=1,证明AD⊥AM,AD⊥AC,∴AM,AD,AC两两垂直,以A为坐标原点,AD,AC,AM分别为x,y,z轴,求出相关点的坐标,求出平面CC1D的法向量,平面MAD的一个法向量,利用空间向量的数量积求解即可.
【考点精析】认真审题,首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行).


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足
满足![]() ,且
,且![]() 的最小值是
的最小值是![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有唯一实数根,求实数
上有唯一实数根,求实数![]() 的取值范围;
的取值范围;
(3)函数![]() ,对任意
,对任意![]() 都有
都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知t为实数,函数![]() ,其中
,其中![]()
(1)若![]() ,求
,求![]() 的取值范围。
的取值范围。
(2)当![]() 时,
时,![]() 的图象始终在
的图象始终在![]() 的图象的下方,求t的取值范围;
的图象的下方,求t的取值范围;
(3)设![]() ,当
,当![]() 时,函数
时,函数![]() 的值域为
的值域为![]() ,若
,若![]() 的最小值为
的最小值为![]() ,求实数a的值.
,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在区间(0,+∞)内的单调函数,且对x∈(0,∞),都有f[f(x)﹣lnx]=e+1,设f′(x)为f(x)的导函数,则函数g(x)=f(x)﹣f′(x)的零点个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图甲所示,放在水平地面上的物体,受到方向不变的水平推力F的作用,F的大小与时间t的关系和物体运动速度v与时间t的关系如图乙所示.下列判断正确的是:
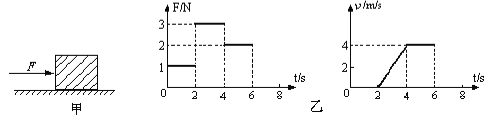
A.t=3s时,物体受到力的合力为零
B.t=6s时,将F撤掉,物体立刻静止
C.2s~4s内物体所受摩擦力逐渐增大
D.t=1s时,物体所受摩擦力是1N
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为了保护环境,减少空气污染,某空气净化器制造厂,决定投入生产某种惠民型的空气净化器.根据以往的生产销售经验得到年生产销售的统计规律如下:①年固定生产成本为2万元;②每生产该型号空气净化器1百台,成本增加1万元;③年生产x百台的销售收入 (万元).假定生产的该型号空气净化器都能卖出(利润=销售收入﹣生产成本).
(万元).假定生产的该型号空气净化器都能卖出(利润=销售收入﹣生产成本).
(1)为使该产品的生产不亏本,年产量x应控制在什么范围内?
(2)该产品生产多少台时,可使年利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com