
分析 (1)求得直线AB的方程,利用点到直线的距离公式求得c的值,根据三角形的面积公式ab=$\sqrt{5}$,由a2=b2+c2,即可求得a和b的值,求得椭圆方程;
(2)设直线l的方程,求得O到直线l的距离d,代入椭圆方程,利用弦长公式,求得m和n,利用基本不等式的性质,即可求得t的值,求得直线l的方程.
解答 解:(1)设F1坐标为(-c,0),F2坐标为(c,0),(c>0),
则直线AB的方程为$y=\sqrt{3}({x-c})$,即$\sqrt{3}x-y-\sqrt{3}c=0,\frac{{|{-\sqrt{3}c-\sqrt{3}c}|}}{{\sqrt{3+1}}}=2\sqrt{3},c=2$;
又$S=\frac{1}{2}•2a•2b=2\sqrt{5}$,
∴$ab=\sqrt{5}$,解得:a2=5,b2=1,
∴椭圆D的方程为$\frac{x^2}{5}+{y^2}=1$;
(2)易知直线l的斜率不为0,可设直线l的方程为x=ty+2,则圆心C到直线l的距离为$d=\frac{{|{2t}|}}{{\sqrt{{t^2}+1}}}$,
∴$n=2\sqrt{{2^2}-{d^2}}=\frac{4}{{\sqrt{{t^2}+1}}},\left\{\begin{array}{l}x=ty+2\\ \frac{x^2}{5}+{y^2}=1\end{array}\right.$,得(t2+5)y2+4ty-1=0,
∴$m=\sqrt{1+{t^2}}|{{y_1}-{y_2}}|=\frac{{2\sqrt{5}({{t^2}+1})}}{{{t^2}+5}}$,
∴$m•n=\frac{{8\sqrt{5}•\sqrt{{t^2}+1}}}{{{t^2}+5}}=\frac{{8\sqrt{5}}}{{\sqrt{{t^2}+1}+\frac{4}{{\sqrt{{t^2}+1}}}}}≤2\sqrt{5}$(当且仅当$\sqrt{{t^2}+1}=\frac{4}{{\sqrt{{t^2}+1}}}$,即$t=±\sqrt{3}$时,等号成立),
∴直线方程为$x-\sqrt{3}y-2=0$或$x+\sqrt{3}y-2=0$.
点评 本题考查椭圆的标准方程,点到直线的距离公式,考查韦达定理,弦长公式及基本不等式的性质,考查计算能力,属于中档题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:解答题
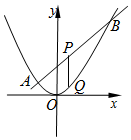 已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.
已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
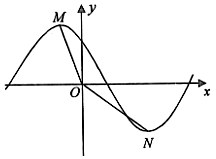 将函数y=$\sqrt{3}$sin($\frac{π}{4}$x)的图象向左平移3个单位,得函数y=$\sqrt{3}$sin($\frac{π}{4}$x+φ)(|φ|<π)的图象(如图),点M,N分别是函数f(x)图象上y轴两侧相邻的最高点和最低点,设∠MON=θ,则tan(φ-θ)的值为( )
将函数y=$\sqrt{3}$sin($\frac{π}{4}$x)的图象向左平移3个单位,得函数y=$\sqrt{3}$sin($\frac{π}{4}$x+φ)(|φ|<π)的图象(如图),点M,N分别是函数f(x)图象上y轴两侧相邻的最高点和最低点,设∠MON=θ,则tan(φ-θ)的值为( )| A. | 1-$\sqrt{3}$ | B. | 2-$\sqrt{3}$ | C. | 1+$\sqrt{3}$ | D. | -2+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com