
���� ������a��c��ֵ�����b���Ӷ������Բ�ķ��̼��ɣ�
��������ֱ�ߺ���Բ�ķ��̣����ݽ���ĸ����ж�m�ķ�Χ����AB���е�ΪE��x0��y0�������x0=$\frac{{{x}_{1}+x}_{2}}{2}$=-$\frac{3m}{4}$��y0=x0+m=$\frac{m}{4}$����m=2ʱ�����ֱ�߷�����y=-x-1�������Ӧ��x��ֵ����m=-2ʱ�����ֱ�߷�����y=-x+1�������Ӧ��x��ֵ���ɣ�
��� �⣺��������֪��a=2$\sqrt{3}$����$c=2\sqrt{2}$
��b2=a2-c2=4
����Բ�ķ���Ϊ$\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{4}$=1��
������$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{12}+\frac{{y}^{2}}{4}=1}\end{array}\right.$����4x2+6mx+3m2-12=0 ��
��ֱ��l����Բ���ڲ�ͬ����A��B�����=36m2-16��3m2-12����0��
��m2��16��
��A��x1��y1����B��x2��y2������x1��x2�Ƿ��̢ٵ�������
��x1+x2=-$\frac{3m}{2}$��${x_1}•{x_2}=\frac{{3{m^2}-12}}{4}$��
��$|{AB}|=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|=\sqrt{2}��\sqrt{\frac{9}{4}{m^2}-��3{m^2}-12��}=\sqrt{2}��\sqrt{-\frac{3}{4}{m^2}+12}$��
����$|{AB}|=3\sqrt{2}$����$-\frac{3}{4}{m^2}+12=9$����֮y=-x+1
������֪����PΪ�߶�AB���д�����ֱ��y=2�Ľ��㣮
��AB���е�ΪE��x0��y0������x0=$\frac{{{x}_{1}+x}_{2}}{2}$=-$\frac{3m}{4}$��y0=x0+m=$\frac{m}{4}$��
?��m=2ʱ��$E��-\frac{3}{2}��\frac{1}{2}��$
���ʱ���߶�AB���д��߷���Ϊy-$\frac{1}{2}$=-��x+$\frac{3}{2}$������y=-x-1��
��y=2����x0=-3��
?��m=-2ʱ��E��$\frac{3}{2}$��-$\frac{1}{2}$����
���ʱ���߶�m=1���д��߷���Ϊy+$\frac{1}{2}$=-��x-$\frac{3}{2}$������y=-x+1��
��$��0��\frac{1}{2}��$����x0=-1��
���� ���⿼��������Բ�ķ������⣬����ֱ�ߺ���Բ��λ�ù�ϵ�Լ�Τ�ﶨ����Ӧ�á��е����깫ʽ����һ���ۺ��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��cos����sin���� | B�� | ��cos����-sin���� | C�� | ��sin����-cos���� | D�� | ��sin����cos���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
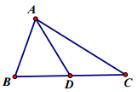 ��֪��ABC�У���DΪBC�е㣬AB=2��AC=4��
��֪��ABC�У���DΪBC�е㣬AB=2��AC=4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com