
【题目】已知函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)讨论函数![]() 的单调性.
的单调性.
【答案】(1) ![]() ;(2) 当
;(2) 当![]() 时,
时,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 上单调递增.
上单调递增.
【解析】试题分析:(1)利用导数的几何意义求点![]() 处的切线方程;(2)
处的切线方程;(2)![]() ,
,
即分析![]() 的符号情况,先抓二次项系数,进而分析抛物线与x轴的交点情况,即可得到函数
的符号情况,先抓二次项系数,进而分析抛物线与x轴的交点情况,即可得到函数![]() 的单调性.
的单调性.
试题解析:
(1)当![]() 时,
时,![]() ,则
,则![]() ,
,
又![]() ,
,
所以曲线![]() 在
在![]() 处的切线方程为:
处的切线方程为:![]() ,即
,即![]() ;
;
(2)![]() ,
,
令![]() ,
,
①当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() 在
在![]() 单调递减;
单调递减;
②当![]() 时,二次函数
时,二次函数![]() 的图象开口方向向下,
的图象开口方向向下,
其图象对称轴![]() ,且
,且![]() ,
,
所以当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 单调递减;
单调递减;
③当![]() 时,二次函数开口向上,其图象对称轴
时,二次函数开口向上,其图象对称轴![]() .
.
![]() ,其图象与
,其图象与![]() 轴正半轴交点为
轴正半轴交点为![]() ,
,
所以当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减.
上单调递减.
当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,
综上所述:当![]() 时,
时,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 上单调递增.
上单调递增.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知在四棱锥S﹣ABCD中,底面ABCD是菱形,且∠BCD=60°,侧面SAB是正三角形,且面SAB⊥面ABCD,F为SD的中点. 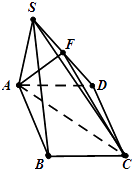
(1)证明:SB∥面ACF;
(2)求面SBC与面SAD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若(2x+ ![]() )100=a0+a1x+a2x2+…+a100x100 , 则(a0+a2+a4+…+a100)2﹣(a1+a3+a5+…+a99)2的值为( )
)100=a0+a1x+a2x2+…+a100x100 , 则(a0+a2+a4+…+a100)2﹣(a1+a3+a5+…+a99)2的值为( )
A.1
B.﹣1
C.0
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行“庆元旦”教工羽毛球单循环比赛(任意两个参赛队伍只比赛一场),有高一、高二、高三共三个队参赛,高一胜高二的概率为![]() ,高一胜高三的概率为
,高一胜高三的概率为![]() ,高二胜高三的概率为
,高二胜高三的概率为![]() ,每场胜负相互独立,胜者记1分,负者记0分,规定:积分相同时,高年级获胜.
,每场胜负相互独立,胜者记1分,负者记0分,规定:积分相同时,高年级获胜.
(1)若高三获得冠军的概率为![]() ,求
,求![]() ;
;
(2)记高三的得分为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(﹣2,2),函数g(x)=f(x﹣1)+f(3﹣2x).
(1)求函数g(x)的定义域;
(2)若f(x)是奇函数且在定义域内单调递减,求不等式g(x)≤0的解集
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数.他们研究过如图所示的三角形数:
将三角形数1,3,6,10,…记为数列{an},将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn},可以推测:
(1)b5=;
(2)b2n﹣1= . 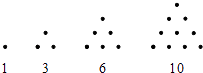
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com