
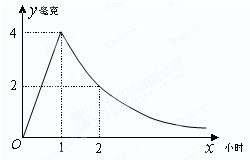
 病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量y=Max(毫克)与时间y=Max(小时)满足:前1小时内成正比例递增,1小时后按指数型函数y=Max(M,a为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量y=Max(毫克)与时间y=Max(小时)满足:前1小时内成正比例递增,1小时后按指数型函数y=Max(M,a为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 8 |
| 31 |
| 8 |
|
|
| 1 |
| 2 |
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 8 |
| 31 |
| 8 |
| 1 |
| 8 |
| 31 |
| 8 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
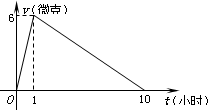 某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y与时间t之间近似满足如图所示的曲线.
某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y与时间t之间近似满足如图所示的曲线.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
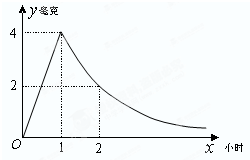 病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量y=Max(毫克)与时间y=Max(小时)满足:前1小时内成正比例递增,1小时后按指数型函数y=Max(M,a为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量y=Max(毫克)与时间y=Max(小时)满足:前1小时内成正比例递增,1小时后按指数型函数y=Max(M,a为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省宿迁市沭阳高中高一(上)期中数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com