练习册

  • 练习册
  • 试题
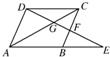
    精英家教网 > 高中数学 > 题目详情
    精英家教网如图，在?ABCD中，E是AB延长线上一点，DE交AC于G，交BC于F．
    求证：（1）DG2=GE•GF；
    （2）
    CF
    CB
    =
    AB
    AE
    ．
    分析：（1）根据平行四边形两条对边平行，得到两对相似三角形．写出对应边成比例，得到两个比例式中各有两条线段的比相等，根据等量代换得到比例式，转化成乘积式，得到结论．
    （2）做法同一类似，根据两条线段平行，根据平行得到对应线段成比例，在两个比例式中出现有一个比例相等，利用等量代换，得到结论．
    解答：证明：（1）∵CD∥AE，
    ∴
    DG
    GE
    =
    CG
    AG
    ．
    又∵AD∥CF，
    ∴
    GF
    DG
    =
    CG
    AG
    ．
    ∴
    DG
    GE
    =
    GF
    DG
    ，
    即DG2=GE•GF．
    （2）∵BF∥AD，
    ∴
    AB
    AE
    =
    DF
    DE
    ．①
    又∵CD∥BE，∴
    CF
    CB
    =
    DF
    DE
    ．②
    由①②可得
    CF
    CB
    =
    AB
    AE
    ．
    点评：本题考查平行线分线段成比例定理，在题目中连续使用成比例定理，有两次使用等量代换，是一个比较典型的题目，实际上证明线段成比例是学习中的难点．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

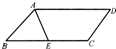    精英家教网如图，在?ABCD中，AD=5，AB=3，AE平分∠BAD交BC边于点E，则线段BE，EC的长度分别为（　　）
    A、3和2B、2和3C、4和1D、1和4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图2,在ABCD中,E是AD的中点,AC、BD交于O,则与△ABE面积相等的三角形有…（　　）

    A.5个                   B.6个                C.7个                   D.8个            D.梯形

    图2

    查看答案和解析>>

    科目：高中数学 来源：2013年湖北新洲、红安、麻城一中高三上学期期末考文科数学试卷（解析版） 题型：解答题

    (本小题满分12分)

    如图，在□ABCD中，∠DAB=60°，AB=2，AD="4." 将△CBD沿BD折起到△EBD的位置，使平面EBD⊥平面ABD.

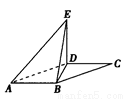
    (1)求证：AB⊥DE；

    (2)求三棱锥E—ABD的侧面积.

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年福建省厦门市高三10月月考文科数学试卷 题型：填空题

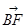    如图，在□ABCD中，E、F分别是BC，DC的中点，，用a，b表示和。

    则=            ,=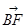        

     

     

    查看答案和解析>>

    同步练习册答案