
【题目】已知函数![]() =
=![]() ,若对于任意实数
,若对于任意实数![]() ,不等式
,不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是_________;
的取值范围是_________;
【答案】(0,1)
【解析】
由题意设g(x)=ex﹣e﹣x﹣2x,x∈R,则g(x)是定义域R上的奇函数,且为增函数;问题等价于g(x2+a)>g(﹣2ax)恒成立,得出x2+a>﹣2ax,利用判别式△<0求得实数a的取值范围.
函数f(x)=ex﹣e﹣x﹣2x+1,x∈R;可设g(x)=ex﹣e﹣x﹣2x,x∈R;
则f(x)=g(x)+1,
且g(﹣x)=e﹣x﹣ex+2x=﹣(ex﹣e﹣x﹣2x)=﹣g(x),
∴g(x)是定义域R上的奇函数;又g′(x)=ex+e﹣x﹣2≥0恒成立,
∴g(x)是定义域R上的增函数;
∴不等式f(x2+a)+f(2ax)>2恒成立,
化为g(x2+a)+g(2ax)+2>2恒成立,
即g(x2+a)>﹣g(2ax)=g(﹣2ax)恒成立,∴x2+a>﹣2ax恒成立,
即x2+2ax+a>0恒成立;∴△=4a2﹣4a<0,
解得0<a<1,∴实数a的取值范围是(0,1).
故答案为:(0,1).


科目:高中数学 来源: 题型:
【题目】某农科所对冬季昼夜温差![]() (
(![]() )与某反季节新品种大豆种子的发芽数(颗)之间的关系进行分析研究,他们分别记录了12月1日至12月5日每天的昼夜温差与实验室每天每100颗种子的发芽数,得到的数据如下表所示:
)与某反季节新品种大豆种子的发芽数(颗)之间的关系进行分析研究,他们分别记录了12月1日至12月5日每天的昼夜温差与实验室每天每100颗种子的发芽数,得到的数据如下表所示:
12月1日 | 12月2日 | 12月3日 | 12月4日| | 12月5日 | |
| 10 | 11 | 13 | 12 | 8 |
| 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是:先从这5组数据中选取3组求线性回归方程,剩下的2组数据用于线性回归方程的检验.
(1)请根据12月2日至12月4日的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所选的验证数据的误差不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得到的线性回归方程是否可靠?如果可靠,请预测温差为14![]() 时种子的发芽数;如果不可靠,请说明理由.
时种子的发芽数;如果不可靠,请说明理由.
参考公式:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
B.对于命题![]() :
:![]() ,使得
,使得![]() ,则
,则![]() :
:![]() 均有
均有![]()
C.若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题
均为假命题
D.命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() +1(
+1(![]() )在(0,+∞)内有且只有一个零点,则
)在(0,+∞)内有且只有一个零点,则![]() 在[﹣1,1]上的值域为
在[﹣1,1]上的值域为
A. [﹣4,0] B. [﹣4,1] C. [﹣1,3] D. [﹣![]() ,12]
,12]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲乙两组学生,分别参加某项体能测试,所得成绩的茎叶图如图.规定测试成绩大于等于90分为优秀,80至89分为良好,60至79分为合格,60分以下为不合格.
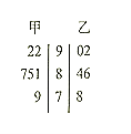
(1)现从甲组数据中抽取一名学生的成绩,有放回地抽取6次,记抽到优秀成绩的次数为X,求![]() ;
;
(2)从甲、乙两组学生中任取3名学生,记抽中成绩优秀的学生数为Y,求Y的概率分布与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 中有:①若
中有:①若![]() ,则
,则![]() ;②若
;②若![]() ,则
,则![]() —定为等腰三角形;③若
—定为等腰三角形;③若![]() ,则
,则![]() —定为直角三角形;④若
—定为直角三角形;④若![]() ,且该三角形有两解,则
,且该三角形有两解,则![]() 的范围是
的范围是![]() .以上结论中正确的个数有( )
.以上结论中正确的个数有( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一座小岛距离海岸线上最近的点P的距离是3 km,从点P沿海岸正东12 km处有一个渔村.
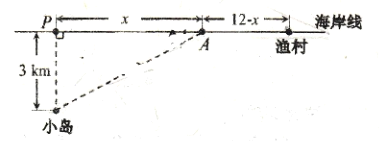
(1)假设一个人驾驶的小船的平均速度为![]() ,步行的速度是
,步行的速度是![]() .y(单位:h)表示他从小岛到渔村的时间,x(单位:km)表示此人将船停在海岸处A与P点的距离.请将y表示为x的函数,并写出定义域;
.y(单位:h)表示他从小岛到渔村的时间,x(单位:km)表示此人将船停在海岸处A与P点的距离.请将y表示为x的函数,并写出定义域;
(2)在(1)的条件下,是否有一个停船的位置使得从小岛到渔村花费的时间最少?说明理由.(![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com