
【题目】设函数![]() .
.
(1)当![]() 时,解方程
时,解方程![]() ;
;
(2)当![]() 时,若不等式
时,若不等式![]() 在
在![]() 上恒成立,求实数a的取值范围;
上恒成立,求实数a的取值范围;
(3)若a为常数,且函数![]() 在区间
在区间![]() 上存在零点,求实数b的取值范围.
上存在零点,求实数b的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)当![]() 时,原方程化为
时,原方程化为![]() ,先解得
,先解得![]() 即可得结果;(2)不等式
即可得结果;(2)不等式![]() 在
在![]() 上恒成立,等价于
上恒成立,等价于![]() 在
在![]() 上恒成立,求出函数
上恒成立,求出函数![]() 的最大值即可得结果;(3)函数
的最大值即可得结果;(3)函数![]() 在
在![]() 上存在零点,即方程
上存在零点,即方程![]() 在
在![]() 上有解,分类求出
上有解,分类求出![]() 的值域即可得结果.
的值域即可得结果.
试题解析:(1)当![]() 时,
时, ![]() ,所以方程即为:
,所以方程即为: ![]()
解得: ![]() 或
或![]() (舍),所以
(舍),所以![]() ;
;
(2)当![]() 时,若不等式
时,若不等式![]() 在
在![]() 上恒成立;
上恒成立;
当![]() 时,不等式恒成立,则
时,不等式恒成立,则![]() ;
;
当![]() 时,
时, ![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,
上恒成立,
因为![]() 在
在![]() 上单调增,
上单调增, ![]() ,
, ![]() ,则
,则![]() ,
,
得![]() ;则实数
;则实数![]() 的取值范围为
的取值范围为![]() ;
;
(3)函数![]() 在
在![]() 上存在零点,即方程
上存在零点,即方程![]() 在
在![]() 上有解;
上有解;
设![]()
当![]() 时,则
时,则![]() ,且
,且![]() 在
在![]() 上单调增,
上单调增,
所以![]() ,
, ![]() ,
,
则当![]() 时,原方程有解,
时,原方程有解,
则![]() ;
;
当![]() 时,
时, ![]() ,
,
![]() 在
在![]() 上单调增,在
上单调增,在![]() 上单调减,在
上单调减,在![]() 上单调增;
上单调增;
当![]() ,即
,即![]() 时,
时, ![]() ,
,
则当![]() 时,原方程有解,则
时,原方程有解,则![]() ;
;
当![]() ,即
,即![]() 时,
时, ![]() ,
,
则当![]() 时,原方程有解,则
时,原方程有解,则![]() ;
;
当![]() 时,
时, 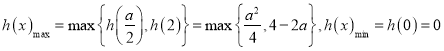 ,
,
当![]() ,即则
,即则![]() 时,
时, ![]() ,
,
则当![]() 时,原方程有解,则
时,原方程有解,则![]() ;
;
当![]() ,即则
,即则![]() 时,
时, ![]() ,
,
则当![]() 时,原方程有解,则
时,原方程有解,则![]() ;
;
综上,当![]() 时,实数
时,实数![]() 的取值范围为
的取值范围为![]() ;
;
当![]() 时,实数
时,实数![]() 的取值范围为
的取值范围为![]() ;
;
当![]() 时,实数
时,实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】某市一家庭今年一月份、二月份和三月份煤气用量和支付费用如下表所示:
月份 | 用气量(立方米) | 煤气费(元) |
1 | 4 | 4.00 |
2 | 25 | 14.00 |
3 | 35 | 19.00 |
该市煤气收费的方法是:煤气费=基本费+超额费+保险费.
若每月用气量不超过最低额度A(A>4)立方米时,只付基本费3元和每户每月定额保险费C(0<C≤5)元;若用气量超过A立方米时,超过部分每立方米付B元.
(1)根据上面的表格求A,B,C的值;
(2)记该家庭第四月份用气为x立方米,求应交的煤气费y元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出30个数:1,2,4,7,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,依此类推.要计算这30个数的和,现已给出了该问题算法的程序框图(如图所示),请在图中判断框内①处和执行框中的②处填上合适的语句,使之能完成该题算法功能.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数  下列四个命题: ①f(f(1))>f(3);
下列四个命题: ①f(f(1))>f(3);
②x0∈(1,+∞), ![]() ;
;
③f(x)的极大值点为x=1;
④x1 , x2∈(0,+∞),|f(x1)﹣f(x2)|≤1
其中正确的有 . (写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学从某次考试成绩中抽取若干名学生的分数,并绘制成如图所示的频率分布直方图,样本数据分组为[50,60),[60,70),[70,80),[80,90),[90,100].若用分层抽样的方法从样本中抽取分数在[80,100]范围内的数据16个,则其中分数在[90,100]范围内的样本数据有 ( )

A. 5个 B. 6个
C. 8个 D. 10个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点O为坐标原点,椭圆 ![]() 的右顶点为A,上顶点为B,过点O且斜率为
的右顶点为A,上顶点为B,过点O且斜率为 ![]() 的直线与直线AB相交M,且
的直线与直线AB相交M,且 ![]() .
.
(Ⅰ)求证:a=2b;
(Ⅱ)PQ是圆C:(x﹣2)2+(y﹣1)2=5的一条直径,若椭圆E经过P,Q两点,求椭圆E的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A、B、C的对边分别为a、b、c,且a>c,已知![]() =2,cosB=
=2,cosB=![]() ,b=3,求:
,b=3,求:
(1)a和c的值;
(2)cos(B-C)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x2+bx+c,不等式f(x)<0的解集是(0,5),若对于任意x∈[2,4],不等式f(x)+t≤2恒成立,则t的取值范围为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com