
【题目】某地区上年度电价为![]() 元/kWh,年用电量为
元/kWh,年用电量为![]() kWh.本年度计划将电价降低到0.55元/ kWh到0.75元/ kWh之间,而用户期望电价为0.40元/ kWh.经测算,下调电价后新增用电量与实际电价与用户的期望电价的差成反比(比例系数为
kWh.本年度计划将电价降低到0.55元/ kWh到0.75元/ kWh之间,而用户期望电价为0.40元/ kWh.经测算,下调电价后新增用电量与实际电价与用户的期望电价的差成反比(比例系数为![]() ),该地区电力的成本价为0.30元/ kWh.
),该地区电力的成本价为0.30元/ kWh.
(1)写出本年度电价下调后,电力部门的收益![]() 与实际电价
与实际电价![]() 之间的函数关系式;
之间的函数关系式;
(2)设![]() =
=![]() ,当电价最低定为多少时仍可保证电力部门的收益比上一年至少增长20%?(注:收益=实际电量×(实际电价-成本价))
,当电价最低定为多少时仍可保证电力部门的收益比上一年至少增长20%?(注:收益=实际电量×(实际电价-成本价))
科目:高中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.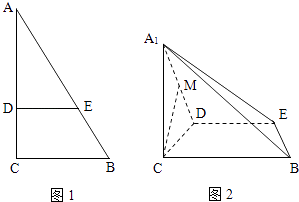
(1)求证:A1C⊥平面BCDE;
(2)若M是A1D的中点,求CM与平面A1BE所成角的大小;
(3)线段BC上是否存在点P,使平面A1DP与平面A1BE垂直?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点的序列An(xn,0),n∈N*,其中x1=0,x2=a(a>0),A3是线段A1A2的中点,A4是线段A2A3的中点,……,An是线段An-2An-1的中点,……
(1)写出xn与xn-1,xn-2之间的关系式(n≥3);
(2)设an=xn+1-xn,计算a1,a2,a3,由此推测数列{an}的通项公式,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”,彰显出中国式创新的强劲活力.某移动支付公司从我市移动支付用户中随机抽取100名进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 10 | 8 | 7 | 3 | 2 | 15 |
女 | 5 | 4 | 6 | 4 | 6 | 30 |
合计 | 15 | 12 | 13 | 7 | 8 | 45 |
(1)把每周使用移动支付超过3次的用户称为“移动支付活跃用户”,由以上数据完成下列2×2列联表,并判断能否在犯错误的概率不超过0.005的前提下,认为“移动支付活跃用户”与性别有关?
移动支付活跃用户 | 非移动支付活跃用户 | 总计 | |
男 | |||
女 | |||
总计 | 100 |
(2)把每周使用移动支付6次及6次以上的用户称为“移动支付达人”,视频率为概率,在我市所有“移动支付达人”中,随机抽取4名用户.为了鼓励男性用户使用移动支付,对抽出的男“移动支付达人”每人奖励300元,记奖励总金额为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附公式及表如下:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构通过对某企业今年的生产经营情况的调查,得到每月利润![]() (单位:万元)与相应月份数
(单位:万元)与相应月份数![]() 的部分数据如表:
的部分数据如表:
| 1 | 4 | 7 | 12 |
| 229 | 244 | 241 | 196 |
(1)根据如表数据,请从下列三个函数中选取一个恰当的函数描述![]() 与
与![]() 的变化关系,并说明理由,
的变化关系,并说明理由,![]() ,
,![]() ,
,![]() ;
;
(2)利用(1)中选择的函数,估计月利润最大的是第几个月,并求出该月的利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() (a>b>0)的左焦点F1与抛物线y2=﹣4x的焦点重合,椭圆E的离心率为
(a>b>0)的左焦点F1与抛物线y2=﹣4x的焦点重合,椭圆E的离心率为 ![]() ,过点M (m,0)(m>
,过点M (m,0)(m> ![]() )作斜率不为0的直线l,交椭圆E于A,B两点,点P(
)作斜率不为0的直线l,交椭圆E于A,B两点,点P( ![]() ,0),且
,0),且 ![]() 为定值.
为定值.
(Ⅰ)求椭圆E的方程;
(Ⅱ)求△OAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用收集到的6组数据对![]() 制作成如图所示的散点图(点旁的数据为该点坐标),并由最小二乘法计算得到回归直线
制作成如图所示的散点图(点旁的数据为该点坐标),并由最小二乘法计算得到回归直线![]() 的方程:
的方程:![]() ,相关系数为
,相关系数为![]() ,相关指数为
,相关指数为![]() ;经过残差分析确定点
;经过残差分析确定点![]() 为“离群点”(对应残差过大的点),把它去掉后,再用剩下的5组数据计算得到回归直线
为“离群点”(对应残差过大的点),把它去掉后,再用剩下的5组数据计算得到回归直线![]() 的方程:
的方程:![]() ,相关系数为
,相关系数为![]() ,相关指数为
,相关指数为![]() .则以下结论中,不正确的是( )
.则以下结论中,不正确的是( )

A. ![]() ,
,![]() B.
B. ![]() ,
,![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com