
ΓΨΧβΡΩΓΩΙζΡΎΡ≥÷ΣΟϊ¥σ―ß”–Ρ–…ζ14000»ΥΘ§≈°…ζ10000»Υ.ΗΟ–ΘΧε”ΐ―ß‘ΚœκΝΥΫβ±Ψ–Θ―ß…ζΒΡ‘ΥΕ·Ή¥ΩωΘ§ΗυΨί–‘±π≤…»ΓΖ÷≤ψ≥ι―υΒΡΖΫΖ®¥”»Ϊ–Θ―ß…ζ÷–≥ι»Γ120»ΥΘ§Ά≥ΦΤΥϊΟ«ΤΫΨυΟΩΧλ‘ΥΕ·ΒΡ ±ΦδΘ®“―÷ΣΗΟ–Θ―ß…ζΤΫΨυΟΩΧλ‘ΥΕ·ΒΡ ±ΦδΖΕΈß «![]()
![]() Θ©Θ§»γœ¬±μΥυ Ψ.
Θ©Θ§»γœ¬±μΥυ Ψ.
Ρ–…ζΤΫΨυΟΩΧλ‘ΥΕ·ΒΡ ±ΦδΖ÷≤Φ«ιΩωΘΚ

≈°…ζΤΫΨυΟΩΧλ‘ΥΕ·ΒΡ ±ΦδΖ÷≤Φ«ιΩωΘΚ
![]()
Θ®1Θ©ΦΌ…ηΆ§Ήι÷–ΒΡΟΩΗω ΐΨίΨυΩ…”ΟΗΟΉι«χΦδΒΡ÷–Φδ÷Β¥ζΧφΘ§«κΗυΨί―υ±ΨΙάΥψΗΟ–ΘΡ–…ζΤΫΨυΟΩΧλ‘ΥΕ·ΒΡ ±ΦδΘ®ΫαΙϊΨΪ»ΖΒΫ0.1Θ©.
Θ®2Θ©»τΙφΕ®ΤΫΨυΟΩΧλ‘ΥΕ·ΒΡ ±Φδ≤Μ…Ό”Ύ![]() ΒΡ―ß…ζΈΣΓΑ‘ΥΕ·¥ο»ΥΓ±Θ§ΒΆ”Ύ
ΒΡ―ß…ζΈΣΓΑ‘ΥΕ·¥ο»ΥΓ±Θ§ΒΆ”Ύ![]() ΒΡ―ß…ζΈΣΓΑΖ«‘ΥΕ·¥ο»ΥΓ±.
ΒΡ―ß…ζΈΣΓΑΖ«‘ΥΕ·¥ο»ΥΓ±.
Θ®ΔΓΘ©ΗυΨί―υ±ΨΙάΥψΗΟ–ΘΓΑ‘ΥΕ·¥ο»ΥΓ±ΒΡ ΐΝΩΘΜ
Θ®ΔΔΘ©«κΗυΨί…œ ω±μΗώ÷–ΒΡΆ≥ΦΤ ΐΨίΧν–¥œ¬Οφ![]() Ν–ΝΣ±μΘ§≤ΔΆ®ΙΐΦΤΥψ≈–ΕœΡήΖώ‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ0.05ΒΡ«ΑΧαœ¬»œΈΣΓΑ‘ΥΕ·¥ο»ΥΓ±”κ–‘±π”–ΙΊ.
Ν–ΝΣ±μΘ§≤ΔΆ®ΙΐΦΤΥψ≈–ΕœΡήΖώ‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ0.05ΒΡ«ΑΧαœ¬»œΈΣΓΑ‘ΥΕ·¥ο»ΥΓ±”κ–‘±π”–ΙΊ.
≤ΈΩΦΙΪ ΫΘΚ  Θ§Τδ÷–
Θ§Τδ÷–![]() .
.
≤ΈΩΦ ΐΨίΘΚ
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() .Θ®2Θ©Θ®ΔΓΘ©4000Θ®»ΥΘ©.Θ®ΔΔΘ©ΦϊΫβΈω.
.Θ®2Θ©Θ®ΔΓΘ©4000Θ®»ΥΘ©.Θ®ΔΔΘ©ΦϊΫβΈω.
ΓΨΫβΈωΓΩΓΨ ‘ΧβΖ÷ΈωΓΩ(1)ΗυΨίΖ÷≤ψ≥ι―υΦΤΥψ≥ωΡ–…ζ≥ι»Γ![]() ,≈°…ζ≥ι»Γ
,≈°…ζ≥ι»Γ![]() ,”…¥ΥΦΤΥψ≥ω
,”…¥ΥΦΤΥψ≥ω![]() ΒΡ÷Β,≤ΔΦΤΥψ≥ωΡ–…ζΤΫΨυ‘ΥΕ· ±Φδ.(2)(i)‘ΥΕ·¥ο»ΥΒΡ±»άΐΈΣ
ΒΡ÷Β,≤ΔΦΤΥψ≥ωΡ–…ζΤΫΨυ‘ΥΕ· ±Φδ.(2)(i)‘ΥΕ·¥ο»ΥΒΡ±»άΐΈΣ![]() ,Ι Ι≤”–
,Ι Ι≤”–![]() »Υ «‘ΥΕ·¥ο»Υ.(ii)ΗυΨί ΐΨίΝ–≥ωΝΣ±μΚσ,ΦΤΥψ
»Υ «‘ΥΕ·¥ο»Υ.(ii)ΗυΨί ΐΨίΝ–≥ωΝΣ±μΚσ,ΦΤΥψ![]() ,Ι ≤ΜΡή‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ0.05ΒΡ«ΑΧαœ¬»œΈΣΓΑ‘ΥΕ·¥ο»ΥΓ±”κ–‘±π”–ΙΊ.
,Ι ≤ΜΡή‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ0.05ΒΡ«ΑΧαœ¬»œΈΣΓΑ‘ΥΕ·¥ο»ΥΓ±”κ–‘±π”–ΙΊ.
ΓΨ ‘ΧβΫβΈωΓΩ
Θ®1Θ©”…Χβ“βΒΟΘ§≥ι»ΓΒΡΡ–…ζ»Υ ΐΈΣ![]() Θ®»ΥΘ©Θ§≥ι»ΓΒΡ≈°…ζ»Υ ΐΈΣ
Θ®»ΥΘ©Θ§≥ι»ΓΒΡ≈°…ζ»Υ ΐΈΣ![]() Θ®»ΥΘ©Θ§Ι
Θ®»ΥΘ©Θ§Ι ![]() Θ§
Θ§ ![]() .
.
‘ρΙάΥψΗΟ–ΘΡ–…ζΤΫΨυΟΩΧλ‘ΥΕ·ΒΡ ±ΦδΈΣ![]() Θ§
Θ§
Υυ“‘ΗΟ–ΘΡ–…ζΤΫΨυΟΩΧλ‘ΥΕ·ΒΡ ±ΦδΈΣ![]() .
.
Θ®2Θ©Θ®ΔΓΘ©―υ±Ψ÷–ΓΑ‘ΥΕ·¥ο»ΥΓ±Υυ’ΦΒΡ±»άΐ «![]() Θ§
Θ§
Ι ΙάΥψΗΟ–ΘΓΑ‘ΥΕ·¥ο»ΥΓ±”–![]() Θ®»ΥΘ©.
Θ®»ΥΘ©.
Θ®ΔΔΘ©”…Ά≥ΦΤ ΐΨίΒΟΘΚ
ΗυΨί…œ±μΘ§Ω…ΒΟ![]() .
.
Ι ≤ΜΡή‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ0.05ΒΡ«ΑΧαœ¬»œΈΣΓΑ‘ΥΕ·¥ο»ΥΓ±”κ–‘±π”–ΙΊ.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤![]() ΒΡάκ–Ρ¬ ΈΣ
ΒΡάκ–Ρ¬ ΈΣ![]() Θ§«“ΙΐΒψ
Θ§«“ΙΐΒψ![]() .
.

Θ®ΔώΘ©«σΆ÷‘≤ΒΡ±ξΉΦΖΫ≥ΧΘΜ
Θ®ΔρΘ©ΥΡ±Ώ–Έ![]() ΒΡΕΞΒψ‘ΎΆ÷‘≤…œΘ§«“Ε‘Ϋ«œΏ
ΒΡΕΞΒψ‘ΎΆ÷‘≤…œΘ§«“Ε‘Ϋ«œΏ![]() ΓΔ
ΓΔ![]() Ιΐ‘≠Βψ
Ιΐ‘≠Βψ![]() Θ§»τ
Θ§»τ![]() Θ§
Θ§
Θ®1Θ©«σ![]() ΒΡΉν÷ΒΘΜ
ΒΡΉν÷ΒΘΜ
Θ®2Θ©«σ÷ΛΘΜΥΡ±Ώ–Έ![]() ΒΡΟφΜΐΈΣΕ®÷Β.
ΒΡΟφΜΐΈΣΕ®÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®±Ψ–ΓΧβ¬ζΖ÷12Ζ÷Θ©
“―÷Σ≈ΉΈοœΏCΒΡΖΫ≥ΧCΘΚy2="2" p xΘ®pΘΨ0Θ©ΙΐΒψAΘ®1Θ§-2Θ©.
Θ®IΘ©«σ≈ΉΈοœΏCΒΡΖΫ≥ΧΘ§≤Δ«σΤδΉΦœΏΖΫ≥ΧΘΜ
Θ®IIΘ© «Ζώ¥φ‘ΎΤΫ––”ΎOAΘ®OΈΣΉχ±ξ‘≠ΒψΘ©ΒΡ÷±œΏlΘ§ ΙΒΟ÷±œΏl”κ≈ΉΈοœΏC”–ΙΪΙ≤ΒψΘ§«“÷±œΏOA”κlΒΡΨύάκΒ»”Ύ![]() ΘΩ»τ¥φ‘ΎΘ§«σ≥ω÷±œΏlΒΡΖΫ≥ΧΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…ΓΘ
ΘΩ»τ¥φ‘ΎΘ§«σ≥ω÷±œΏlΒΡΖΫ≥ΧΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…ΓΘ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() .
.
Θ®ΔώΘ©…ηΚ· ΐ![]() Θ§ ‘Χ÷¬έΚ· ΐ
Θ§ ‘Χ÷¬έΚ· ΐ![]() ΒΡΒΞΒς–‘ΘΜ
ΒΡΒΞΒς–‘ΘΜ
Θ®ΔρΘ©…ηΚ· ΐ![]()
![]() Θ§«σΚ· ΐ
Θ§«σΚ· ΐ![]() ΒΡΉν–Γ÷Β.
ΒΡΉν–Γ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ[―Γ–ό4-4ΘΚΉχ±ξœΒ”κ≤Έ ΐΖΫ≥Χ]
‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§÷±œΏ
÷–Θ§÷±œΏ![]() ΒΡ≤Έ ΐΖΫ≥ΧΈΣ
ΒΡ≤Έ ΐΖΫ≥ΧΈΣ![]() Θ®
Θ®![]() ΈΣ≤Έ ΐΘ©Θ§‘Ύ“‘÷±Ϋ«Ήχ±ξœΒΒΡ‘≠Βψ
ΈΣ≤Έ ΐΘ©Θ§‘Ύ“‘÷±Ϋ«Ήχ±ξœΒΒΡ‘≠Βψ![]() ΈΣΦΪΒψΘ§
ΈΣΦΪΒψΘ§ ![]() ÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΒΡΦΪΉχ±ξœΒ÷–Θ§«ζœΏ
÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΒΡΦΪΉχ±ξœΒ÷–Θ§«ζœΏ![]() ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ
ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ![]() .
.
Θ®ΔώΘ©«σ«ζœΏ![]() ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΚΆ÷±œΏ
ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΚΆ÷±œΏ![]() ΒΡΤ’Ά®ΖΫ≥ΧΘΜ
ΒΡΤ’Ά®ΖΫ≥ΧΘΜ
Θ®ΔρΘ©»τ÷±œΏ![]() ”κ«ζœΏ
”κ«ζœΏ![]() œύΫΜ”Ύ
œύΫΜ”Ύ![]() Θ§
Θ§ ![]() ΝΫΒψΘ§«σ
ΝΫΒψΘ§«σ![]() ΒΡΟφΜΐ.
ΒΡΟφΜΐ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥Ά§―ß”ΟΓΑΈεΒψΖ®Γ±Μ≠Κ· ΐfΘ®xΘ©ΘΫAsinΘ®ΠΊx+Π’Θ©Θ®ΠΊΘΨ0Θ§|Π’|![]() Θ©‘ΎΡ≥“ΜΗω÷ήΤΎΡΎΒΡΆΦœσ ±Θ§Ν–±μ≤ΔΧν»κΝΥ≤ΩΖ÷ ΐΨίΘ§»γ±μΘΚ
Θ©‘ΎΡ≥“ΜΗω÷ήΤΎΡΎΒΡΆΦœσ ±Θ§Ν–±μ≤ΔΧν»κΝΥ≤ΩΖ÷ ΐΨίΘ§»γ±μΘΚ
ΠΊx+Π’ | 0 |
| Π– |
| 2Π– |
x |
|
| |||
AsinΘ®ΠΊx+Π’Θ© | 0 | 5 | ©¹5 | 0 |
Θ®1Θ©«κΫΪ…œ±μ ΐΨί≤Ι≥δΆξ’ϊΘ§≤Δ÷±Ϋ”–¥≥ωΚ· ΐfΘ®xΘ©ΒΡΫβΈω ΫΘΜ
Θ®2Θ©ΫΪyΘΫfΘ®xΘ©ΆΦœσ…œΥυ”–ΒψœρΉσΤΫ“ΤΠ»Θ®Π»ΘΨ0Θ©ΗωΒΞΈΜ≥ΛΕ»Θ§ΒΟΒΫyΘΫgΘ®xΘ©ΒΡΆΦœσ.»τyΘΫgΘ®xΘ©ΆΦœσΒΡ“ΜΗωΕ‘≥Τ÷––ΡΈΣΘ®![]() Θ§0Θ©Θ§«σΠ»ΒΡΉν–Γ÷Β.
Θ§0Θ©Θ§«σΠ»ΒΡΉν–Γ÷Β.
Θ®3Θ©»τ![]() Θ§«σ
Θ§«σ![]() ΒΡ÷Β.
ΒΡ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
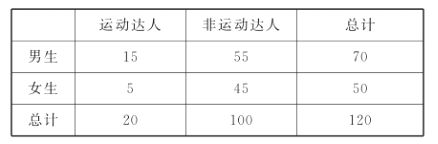
ΓΨΧβΡΩΓΩΡ≥–Θ¥”≤ΈΦ”ΗΏ“ΜΡξΦΕΤΎΡ©ΩΦ ‘ΒΡ―ß…ζ÷–≥ι≥ω60Οϊ―ß…ζΘ§ΫΪΤδ ΐ―ß≥…Φ®Θ®ΨυΈΣ’ϊ ΐΘ©Ζ÷≥…ΝυΕΈ![]() ΚσΘ§Μ≠≥ω»γœ¬≤ΩΖ÷ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ.Ιέ≤λΆΦ–ΈΒΡ–≈œΔΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
ΚσΘ§Μ≠≥ω»γœ¬≤ΩΖ÷ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ.Ιέ≤λΆΦ–ΈΒΡ–≈œΔΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ

Θ®1Θ©«σΒΎΥΡ–ΓΉιΒΡΤΒ¬ Θ§≤Ι»ΪΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§≤Δ«σ―υ±Ψ ΐΨίΒΡ÷Ύ ΐΘ§÷–ΈΜ ΐΘ§ΤΫΨυ ΐ![]() ΚΆΖΫ≤ν
ΚΆΖΫ≤ν![]() Θ§Θ®Ά§“ΜΉι÷–ΒΡ ΐΨί”ΟΗΟ«χΦδΒΡ÷–Βψ÷ΒΉς¥ζ±μΘ©ΘΜ
Θ§Θ®Ά§“ΜΉι÷–ΒΡ ΐΨί”ΟΗΟ«χΦδΒΡ÷–Βψ÷ΒΉς¥ζ±μΘ©ΘΜ
Θ®2Θ©¥”±Μ≥ι»ΓΒΡ ΐ―ß≥…Φ® «![]() Ζ÷“‘…œΘ®Αϋά®
Ζ÷“‘…œΘ®Αϋά®![]() Ζ÷Θ©ΒΡ―ß…ζ÷–―ΓΝΫ»ΥΘ§«σΥϊΟ«‘ΎΆ§“ΜΖ÷ ΐΕΈΒΡΗ≈¬ ΘΜ
Ζ÷Θ©ΒΡ―ß…ζ÷–―ΓΝΫ»ΥΘ§«σΥϊΟ«‘ΎΆ§“ΜΖ÷ ΐΕΈΒΡΗ≈¬ ΘΜ
Θ®3Θ©ΦΌ…η¥”»Ϊ –≤ΈΦ”ΗΏ“ΜΡξΦΕΤΎΡ©ΩΦ ‘ΒΡ―ß…ζ÷–Θ§»Έ“β≥ι»Γ![]() Ηω―ß…ζΘ§…η’βΥΡΗω―ß…ζ÷– ΐ―ß≥…Φ®ΈΣ
Ηω―ß…ζΘ§…η’βΥΡΗω―ß…ζ÷– ΐ―ß≥…Φ®ΈΣ![]() Ζ÷“‘…œΘ®Αϋά®
Ζ÷“‘…œΘ®Αϋά®![]() Ζ÷Θ©ΒΡ»Υ ΐΈΣ
Ζ÷Θ©ΒΡ»Υ ΐΈΣ![]() Θ®“‘ΗΟ–Θ―ß…ζΒΡ≥…Φ®ΒΡΤΒ¬ ΙάΦΤΗ≈¬ Θ©Θ§«σ
Θ®“‘ΗΟ–Θ―ß…ζΒΡ≥…Φ®ΒΡΤΒ¬ ΙάΦΤΗ≈¬ Θ©Θ§«σ![]() ΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊ.
ΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ«ζœΏ![]() Θ§
Θ§![]() Θ§‘ρœ¬Ν–Ϋα¬έ’ΐ»ΖΒΡ «Θ® Θ©
Θ§‘ρœ¬Ν–Ϋα¬έ’ΐ»ΖΒΡ «Θ® Θ©
A. Α―![]() …œΥυ”–ΒΡΒψœρ”“ΤΫ“Τ
…œΥυ”–ΒΡΒψœρ”“ΤΫ“Τ![]() ΗωΒΞΈΜ≥ΛΕ»Θ§‘ΌΑ―Υυ”–ΆΦœσ…œΗςΒψΒΡΚαΉχ±ξΥθΕΧΒΫ‘≠ά¥ΒΡ
ΗωΒΞΈΜ≥ΛΕ»Θ§‘ΌΑ―Υυ”–ΆΦœσ…œΗςΒψΒΡΚαΉχ±ξΥθΕΧΒΫ‘≠ά¥ΒΡ![]() ±ΕΘ®ΉίΉχ±ξ≤Μ±δΘ©Θ§ΒΟΒΫ«ζœΏ
±ΕΘ®ΉίΉχ±ξ≤Μ±δΘ©Θ§ΒΟΒΫ«ζœΏ![]()
B. Α―![]() …œΥυ”–ΒψœρΉσΤΫ“Τ
…œΥυ”–ΒψœρΉσΤΫ“Τ![]() ΗωΒΞΈΜ≥ΛΕ»Θ§‘ΌΑ―ΥυΒΟΆΦœσ…œΗςΒψΒΡΚαΉχ±ξ…λ≥ΛΒΫ‘≠ά¥ΒΡ3±ΕΘ®ΉίΉχ±ξ≤Μ±δΘ©Θ§ΒΟΒΫ«ζœΏ
ΗωΒΞΈΜ≥ΛΕ»Θ§‘ΌΑ―ΥυΒΟΆΦœσ…œΗςΒψΒΡΚαΉχ±ξ…λ≥ΛΒΫ‘≠ά¥ΒΡ3±ΕΘ®ΉίΉχ±ξ≤Μ±δΘ©Θ§ΒΟΒΫ«ζœΏ![]()
C. Α―![]() …œΗςΒψΒΡΚαΉχ±ξΥθΕΧΒΫ‘≠ά¥ΒΡ
…œΗςΒψΒΡΚαΉχ±ξΥθΕΧΒΫ‘≠ά¥ΒΡ![]() ±ΕΘ®ΉίΉχ±ξ≤Μ±δΘ©Θ§‘ΌΑ―ΥυΒΟΆΦœσ…œΥυ”–ΒΡΒψœρΉσΤΫ“Τ
±ΕΘ®ΉίΉχ±ξ≤Μ±δΘ©Θ§‘ΌΑ―ΥυΒΟΆΦœσ…œΥυ”–ΒΡΒψœρΉσΤΫ“Τ![]() ΗωΒΞΈΜ≥ΛΕ»Θ§ΒΟΒΫ«ζœΏ
ΗωΒΞΈΜ≥ΛΕ»Θ§ΒΟΒΫ«ζœΏ![]()
D. Α―![]() …œΗςΒψΒΡΚαΉχ±ξ…λ≥ΛΒΫ‘≠ά¥ΒΡ3±ΕΘ®ΉίΉχ±ξ≤Μ±δΘ©Θ§‘ΌΑ―ΥυΒΟΆΦœσ…œΥυ”–ΒΡΒψœρΉσΤΫ“Τ
…œΗςΒψΒΡΚαΉχ±ξ…λ≥ΛΒΫ‘≠ά¥ΒΡ3±ΕΘ®ΉίΉχ±ξ≤Μ±δΘ©Θ§‘ΌΑ―ΥυΒΟΆΦœσ…œΥυ”–ΒΡΒψœρΉσΤΫ“Τ![]() ΗωΒΞΈΜ≥ΛΕ»Θ§ΒΟΒΫ«ζœΏ
ΗωΒΞΈΜ≥ΛΕ»Θ§ΒΟΒΫ«ζœΏ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΒψ![]() Θ§‘≤
Θ§‘≤![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() ΒΡΕ·÷±œΏ
ΒΡΕ·÷±œΏ![]() ”κ‘≤
”κ‘≤![]() ΫΜ”Ύ
ΫΜ”Ύ![]() ΝΫΒψΘ§œΏΕΈ
ΝΫΒψΘ§œΏΕΈ![]() ΒΡ÷–ΒψΈΣ
ΒΡ÷–ΒψΈΣ![]() ,
,![]() ΈΣΉχ±ξ‘≠ΒψΘ°
ΈΣΉχ±ξ‘≠ΒψΘ°
(Δώ)«σ![]() ΒΡΙλΦΘΖΫ≥ΧΘΜ
ΒΡΙλΦΘΖΫ≥ΧΘΜ
(Δρ)Β±![]() Θ®
Θ®![]() ≤Μ÷ΊΚœΘ© ±Θ§«σ
≤Μ÷ΊΚœΘ© ±Θ§«σ![]() ΒΡΖΫ≥ΧΦΑ
ΒΡΖΫ≥ΧΦΑ![]() ΒΡΟφΜΐΘ°
ΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com