
 }的前
}的前 项和为
项和为 ,且满足
,且满足 =2-
=2- ,(
,( =1,2,3,…)
=1,2,3,…) }的通项公式;
}的通项公式; }满足
}满足 =1,且
=1,且 ,求数列{
,求数列{ }的通项公式;
}的通项公式; ,求
,求 的前
的前 项和
项和
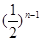 (n∈N*); (Ⅱ) bn=3-2(
(n∈N*); (Ⅱ) bn=3-2(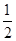 )n-; (Ⅲ)
)n-; (Ⅲ) 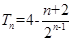 。
。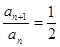 (n∈N*)
(n∈N*)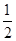 的等比数列.an=
的等比数列.an=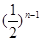 (n∈N*)
(n∈N*)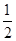 )n-1
)n-1 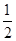
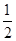 )2
)2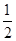 )n-2(n=2,3,…)
)n-2(n=2,3,…) 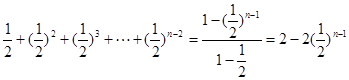
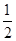 )n-1(n=1,2,3,…)
)n-1(n=1,2,3,…) 
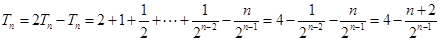
 的形式求通项公式常用累加法。
的形式求通项公式常用累加法。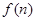 是关于n的一次函数,累加后可转化为等差数列求和;
是关于n的一次函数,累加后可转化为等差数列求和; 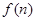 是关于n的二次函数,累加后可分组求和;
是关于n的二次函数,累加后可分组求和; 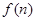 是关于n的指数函数,累加后可转化为等比数列求和;
是关于n的指数函数,累加后可转化为等比数列求和;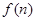 是关于n的分式函数,累加后可裂项求和。
是关于n的分式函数,累加后可裂项求和。

 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
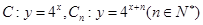 ,从
,从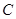 上的点
上的点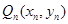 作
作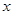 轴的垂线,交
轴的垂线,交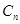 于点
于点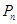 ,再从点
,再从点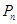 作
作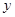 轴的垂线,交
轴的垂线,交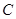 于点
于点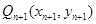 ,
,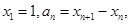
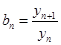 .。
.。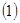 求数列
求数列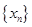 的通项公式;
的通项公式; 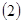 记
记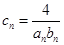 ,数列
,数列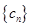 的前
的前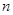 项和为
项和为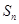 ,试比较
,试比较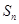 与
与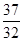 的大小
的大小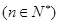 ;
;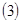 记
记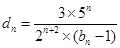 ,数列
,数列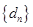 的前
的前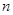 项和为
项和为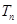 ,试证明:
,试证明: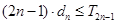 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 为第3项,4为第7项的等差数列的公差;tanB是以
为第3项,4为第7项的等差数列的公差;tanB是以 为第3
为第3| A.等腰三角形 | B.锐角三角形 |
| C.直角三角形 | D.钝角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com