解:(1)由点Q为PN的中点,GQ⊥PN可得:|GP|=|GN|,∴|GM|+|GN|=|MP|=

,而M(-1,0),N(1,0),|MN|=2.
∴|GM|+|GN|>|MN|,∴点G的轨迹是以点M、N为焦点、2

为长轴长的椭圆,其方程为

.
(2)假设存在,如图所示:

∵

,EN⊥AB,∴k
AB=1,即k=1,
∴直线l的方程为y=x+m,设A(x
1,y
1),B(x
2,y
2).
联立

,消去y化为3x
2+4mx+2m
2-2=0,
∵直线l与椭圆C相较于不同的A、B两点,
∴△=16m
2-12(2m
2-2)>0,化为

.(*)
由根与系数的关系可得:

,

.(**)
∵

=(1-x
1,-y
1),

=(-x
2,1-y
2),
∴
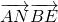
=x
1x
2-x
2+y
1y
2-y
1,
∵AN⊥BE,∴x
1x
2-x
2+y
1y
2-y
1=0,又y
1=x
1+m,y
2=x
2+m,
∴x
1x
2-x
2+(x
1+m)(x
2+m)-(x
1+m)=0,化为2x
1x
2+(m-1)(x
1+x
2)+m
2-m=0,
把(**)代入得

,化为3m
2+m-4=0,
解得m=

或1.
当m=1时,点E与B重合,应舍去.
又

也满足(*),故

.
分析:(1)利用椭圆的定义即可得出;
(2)利用垂心的性质可求出直线AB的斜率,把直线AB的方程与椭圆的方程联立,利用根与系数的关系及垂心的性质即可求出直线AB的方程,进行判断即可.
点评:熟练掌握椭圆的定义、三角形垂心的性质、直线的点斜式、直线方程与椭圆的方程联立得到根与系数的关系是解题的关键.

 如图所示,已知圆M:(x+1)2+y2=8及定点N(1,0),点P是圆M上一动点,点Q为PN的中点,PM上一点G满足
如图所示,已知圆M:(x+1)2+y2=8及定点N(1,0),点P是圆M上一动点,点Q为PN的中点,PM上一点G满足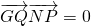
 ,而M(-1,0),N(1,0),|MN|=2.
,而M(-1,0),N(1,0),|MN|=2. 为长轴长的椭圆,其方程为
为长轴长的椭圆,其方程为 .
.
 ,EN⊥AB,∴kAB=1,即k=1,
,EN⊥AB,∴kAB=1,即k=1, ,消去y化为3x2+4mx+2m2-2=0,
,消去y化为3x2+4mx+2m2-2=0, .(*)
.(*) ,
, .(**)
.(**) =(1-x1,-y1),
=(1-x1,-y1), =(-x2,1-y2),
=(-x2,1-y2),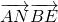 =x1x2-x2+y1y2-y1,
=x1x2-x2+y1y2-y1, ,化为3m2+m-4=0,
,化为3m2+m-4=0, 或1.
或1. 也满足(*),故
也满足(*),故 .
.

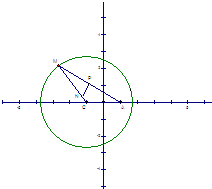 如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆C上一动点,点P在线段AM上,点N在线段CM上,且满足
如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆C上一动点,点P在线段AM上,点N在线段CM上,且满足 如图所示,已知圆M:(x+1)2+y2=8及定点N(1,0),点P是圆M上一动点,点Q为PN的中点,PM上一点G满足
如图所示,已知圆M:(x+1)2+y2=8及定点N(1,0),点P是圆M上一动点,点Q为PN的中点,PM上一点G满足 如图所示,已知椭圆M:
如图所示,已知椭圆M:
