
 ,上部是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱
,上部是一个底面与四棱台的上底面重合,侧面是全等的矩形的四棱柱 .
.
 平面
平面 ;
; ,
,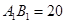 ,
, ,
,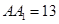 (单位:
(单位: ),每平方厘米的加工处理费为
),每平方厘米的加工处理费为 元,需加工处理费多少元?
元,需加工处理费多少元? 元.
元. ,再证
,再证 平面
平面 ,从而得到
,从而得到 平面
平面 ,在证明
,在证明 平面
平面 的过程中,利用四边形
的过程中,利用四边形 为正方形得到
为正方形得到 ,再由直棱柱的性质得到
,再由直棱柱的性质得到 平面
平面 ,从而得到
,从而得到 ,再利用直线与平面垂直的判定定理得到
,再利用直线与平面垂直的判定定理得到 平面
平面 ;(2)先计算该几何体的表面积,然后利用单价乘以表面积便可以得到加工处理费.
;(2)先计算该几何体的表面积,然后利用单价乘以表面积便可以得到加工处理费. (AB+A1B1)h等腰梯形的高
(AB+A1B1)h等腰梯形的高 (10+20)
(10+20)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).

 、
、 点,并判别MN与平面AEF的位置关系,并给出证明;
点,并判别MN与平面AEF的位置关系,并给出证明; 是线段
是线段 上一点,且
上一点,且 ,问是否存在点
,问是否存在点 使得
使得 ,若存在,求出
,若存在,求出 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com