
分析 (1)利用同角三角函数的基本关系,分类讨论,求得tanα的值.
(2)利用诱导公式,二倍角公式,分类讨论,求得要求式子的值.
解答 解:(1)∵已知-$\frac{π}{2}$<$\frac{α}{2}$<0,∴-π<α<0,
∵sinα=-$\frac{4}{5}$,∴α在第三或第四象限.
当α在第三象限时,cosα=-$\sqrt{{1-sin}^{2}α}$=-$\frac{3}{5}$,tanα=$\frac{sinα}{cosα}$=$\frac{4}{3}$.
当α在第四象限时,cosα=$\sqrt{{1-sin}^{2}α}$=$\frac{3}{5}$,tanα=$\frac{sinα}{cosα}$=-$\frac{4}{3}$.
(2)当α在第三象限时,cos2α+sin($\frac{π}{2}$-α)=2cos2α-1+cosα=2×$\frac{9}{25}$-1-$\frac{3}{5}$=$\frac{22}{25}$.
当α在第四象限时,cos2α+sin($\frac{π}{2}$-α)=2cos2α-1+cosα=2×$\frac{9}{25}$-1+$\frac{3}{5}$=$\frac{8}{25}$.
点评 本题主要考查同角三角函数的基本关系的应用,诱导公式,二倍角公式的应用,属于基础题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
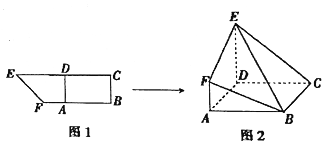 如图所示,在直角梯形BCEF中,∠CBF=∠BCE=90°,A,D分别是BF,CE上的点,AD∥BC,且AB=DE=2BC=2AF(如图1),将四边形ADEF沿AD折起,连结BE、BF、CE(如图2).在折起的过程中,下列结论错误的是④.(填序号)
如图所示,在直角梯形BCEF中,∠CBF=∠BCE=90°,A,D分别是BF,CE上的点,AD∥BC,且AB=DE=2BC=2AF(如图1),将四边形ADEF沿AD折起,连结BE、BF、CE(如图2).在折起的过程中,下列结论错误的是④.(填序号)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (-2,0) | C. | (-2,0] | D. | (-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{17}{9},+∞})$ | B. | $({\frac{17}{9},+∞})$ | C. | (-∞,2] | D. | (-∞,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{7}$ | B. | $\sqrt{10}$ | C. | 4 | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com