
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的长度单位建立坐标系,已知直线l的极坐标方程为2ρcosθ+ρsinθ=3,曲线C的参数方程为 ![]() (α为参数).
(α为参数).
(1)求曲线C的普通方程和直线l的直角坐标方程;
(2)P(1,1),设直线l与曲线C相交于A、B两点,求|PA||PB|的值.
【答案】
(1)解:曲线C的参数方程为 ![]() (α为参数),利用cos2α+sin2α=1可得普通方程:
(α为参数),利用cos2α+sin2α=1可得普通方程: ![]() =1.
=1.
由直线l的极坐标方程为2ρcosθ+ρsinθ=3,可得直角坐标方程:2x+y﹣3=0.
(2)解:由于P(1,1)在直线l上,可得直线l的参数方程: 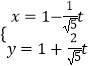 (t为参数),代入椭圆方程可得:
(t为参数),代入椭圆方程可得: ![]() ﹣23=0,
﹣23=0,
∴t1t2=﹣ ![]() ,∴|PA||PB|=|t1t2|=
,∴|PA||PB|=|t1t2|= ![]()
【解析】(1)曲线C的参数方程为 ![]() (α为参数),利用cos2α+sin2α=1可得普通方程.把
(α为参数),利用cos2α+sin2α=1可得普通方程.把 ![]() 代入直线l的极坐标方程为2ρcosθ+ρsinθ=3,可得直角坐标方程.(2)由于P(1,1)在直线l上,可得直线l的参数方程:
代入直线l的极坐标方程为2ρcosθ+ρsinθ=3,可得直角坐标方程.(2)由于P(1,1)在直线l上,可得直线l的参数方程: 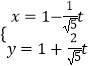 (t为参数),代入椭圆方程可得:
(t为参数),代入椭圆方程可得: ![]() ﹣23=0,利用|PA||PB|=|t1t2|即可得出.
﹣23=0,利用|PA||PB|=|t1t2|即可得出.


科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() 分别为
分别为![]() 的中点,且
的中点,且![]() .
.
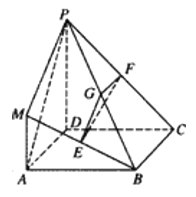
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 与四棱锥
与四棱锥![]() 的体积之比.
的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(170.5,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第1组[157.5,162.5),第2组[162.5,167.5),…,第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图. 
(1)试评估该校高三年级男生的平均身高;
(2)求这50名男生身高在177.5cm以上(含177.5cm)的人数;
(3)在这50名男生身高在177.5cm以上(含177.5cm)的人中任意抽取2人,该2人中身高排名(从高到低)在全省前130名的人数记为ξ,求ξ的分布列和数学期望.
参考数据:若ξ~N(μ,σ2),则P(μ﹣σ<ξ≤μ+σ)=0.6826,P(μ﹣2σ<ξ≤μ+2σ)=0.9544,P(μ﹣3σ<ξ≤μ+3σ)=0.9974.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.若a,b∈R,且a+b>4,则a,b至少有一个大于2
B.若p是q的充分不必要条件,则¬p是¬q的必要不充分条件
C.若命题p:“ ![]() >0”,则¬p:“
>0”,则¬p:“ ![]() ≤0”
≤0”
D.△ABC中,A是最大角,则sin2A>sin2B+sin2C是△ABC为钝角三角形的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
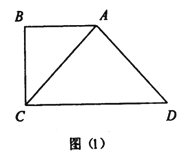
【题目】已知直角梯形![]() ,如图(1)所示,
,如图(1)所示, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,得到几何体
,得到几何体![]() ,如图(2)所示.
,如图(2)所示.
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的大小.
的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x)满足f(x+2)=-f(x),当0≤x≤1时,f(x)=x,
(1)试画出f(x),x∈[-3,5]的图象;
(2)求f(37.5);
(3)常数a∈(0,1),y=a与f(x),x∈[-3,5]的图象相交,求所有交点横坐标之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】太原五中是一所有着百年历史的名校,图1是某一阶段来我校参观学习的外校人数统计茎叶图,第1次到第14次参观学习人数依次记为A1 , A2 , …,A14 , 图2是统计茎叶图中人数在一定范围内的一个算法流程图,那么算法流程图输出的结果是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com