二次函数f(x)=px2+qx+r中实数p、q、r满足
+
+
=0,其中m＞0,
求证:(1)pf(
)＜0；
(2)方程f(x)=0在(0,1)内恒有解.
分析：第(1)问只要对式子适当变形即可证出；第(2)问是利用函数论证方程根的分布问题,只要说明函数f(x)在[0,1]上有异号函数值即可.
证明：(1)pf()=p[p()2+q·+r]
=pm[+
+
]=pm[
-
]
=p2m
=-
,
由于f(x)是二次函数,故p≠0.又m＞0,所以,pf(
)＜0.
(2)由题意,得f(0)=r,f(1)=p+q+r.①当p＞0时,由(1)知f(
)＜0.若r＞0,则f(0)＞0.又f(
)＜0,所以f(x)=0在(0,
)内有解.若r≤0,则f(1)=p+q+r=p+(m+1)(-
-
)+r=
-
＞0.又f(
)＜0,所以f(x)=0在(
,1)内有解.当p＜0时,同理可证.
科目：高中数学 来源： 题型：
查看答案和解析>>
科目：高中数学 来源：2015届新疆乌鲁木齐市高一下学期期中考试数学试卷（解析版） 题型：解答题
)已知二次函数f(x)=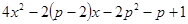
（1）若f（0）>0，求实数p的取值范围
（2）在区间［－1，1］内至少存在一个实数c,使f(c)>0,求实数p的取值范围。
查看答案和解析>>
科目：高中数学 来源：2013届福建省高二上学期期中考试理科数学试卷 题型：解答题
（本小题满分12分）已知关于x的二次函数f(x)＝ax2－4bx＋1.
(1)设集合P＝{－1,1,2,3,4,5}和Q＝{－2，－1,1,2,3,4}，分别从集合P和Q中随机取一个数作为a和b，求函数y＝f(x)在区间[1，＋∞)上是增函数的概率；
增函数的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
=0,其中m>0,求证：
)<0;
二次函数f(x)=px2+qx+r中实数p、q、r满足
=0,其中m>0,求证:
)<0;