
 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立. ,求
,求 的分布列、数学期望和方差.
的分布列、数学期望和方差. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
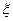 表示所选3人中女生的人数.
表示所选3人中女生的人数.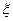 的分布列;
的分布列;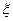 的数学期望;
的数学期望;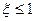 ”的概率.
”的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
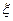 表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值。(1)求
表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值。(1)求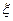 =0对应的事件的概率; (2)求
=0对应的事件的概率; (2)求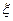 的分布列及数学期望。
的分布列及数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
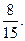 (I)求该小组中女生的人数; (II)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为
(I)求该小组中女生的人数; (II)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为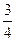 ,每个男生通过的概率均为
,每个男生通过的概率均为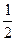 ,现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量
,现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量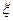 ,求
,求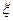 的分布列和数学期望。
的分布列和数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 版本 | 人教A版 | 人教B版 | 苏教版 | 北师大版 |
| 人数 | 20 | 15 | 5 | 10 |
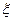 ,求随机变量
,求随机变量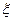 的分布列和数学期望。
的分布列和数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,
, ,
, 的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为
的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为 、
、 ,记
,记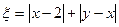 .
. 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率;
取得最大值”的概率; 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 环的概率为
环的概率为 ,乙射击一次命中
,乙射击一次命中 环的概率为
环的概率为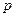 ,若他们独立的射击两次,设乙命中
,若他们独立的射击两次,设乙命中 环的次数为
环的次数为 ,则
,则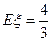 ,
,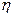 为甲与乙命中
为甲与乙命中 环的次数的差的绝对值.求
环的次数的差的绝对值.求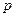 的值及
的值及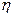 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com