分析:(1)要证线线垂直,关键是证明线面垂直,利用面面垂直可得线面垂直,故可证;
(2)由于面A1DB⊥面DC1B,△ABC是等腰三角形,D为底边AC上中点,可知∠A1DC1是二面角A1-OB-C1的平面角为Rt∠,再将平面A1ACC1放在平面坐标系中,可求.
解答:证明:(1)在斜三棱柱ABC-A
1B
1C
1中,因为A
1在底面ABC上射影落在AC上,则平面A
1ACC
1经过底面ABC的垂线
故侧面A
1C⊥面ABC.
又 BD为等腰△ABC底边AC上中线,则BD⊥AC,从而BD⊥面AC.
∴BD⊥面A
1C
又AA
1?面A
1C,∴AA
1⊥BD
(2)解:在底面ABC,△ABC是等腰三角形,D为底边AC上中点,故DB⊥AC,又面ABC⊥面A
1C
∴DB⊥面A
1C,则DB⊥DA
1,DB⊥DC
1,则∠A
1DC
1是二面角A
1-OB-C
1的平面角
∵面A
1DB⊥面DC
1B,则∠A
1DC
1=Rt∠,将平面A
1ACC
1放在平面坐标系中(如图),

∵侧棱AA
1和底面成60°,
设A
1A=a,则A
1=(
,
a),C
1(
+2
,
a) A(0,0),C(2
,0),AC中点D(
,0),
由
•=0知:(
-
,
a)•(
+
,
a)=0,∴a
2=3,a=
故所求侧棱AA
1长为
点评:本题的考点是点、线、面间的距离计算,考查平面与平面垂直的性质,二面角及其度量,考查计算能力,逻辑思维能力,转化思想.

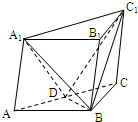 (2007•武汉模拟)如图,在斜三棱柱ABC-A1B1C1中 AB=BC=2,∠ABC=120°,又顶点A1在底面ABC上的射影落在AC上,侧棱AA1与底面成60°的角,D为AC的中点.
(2007•武汉模拟)如图,在斜三棱柱ABC-A1B1C1中 AB=BC=2,∠ABC=120°,又顶点A1在底面ABC上的射影落在AC上,侧棱AA1与底面成60°的角,D为AC的中点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案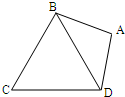 (2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形,
(2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形, (2007•武汉模拟)如图,直线l:y=
(2007•武汉模拟)如图,直线l:y=