
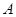 、
、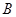 、
、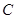 三项活动,且每项活动有且仅有1人参加,甲不参加
三项活动,且每项活动有且仅有1人参加,甲不参加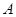 活动,则不同的选派方法有 种.
活动,则不同的选派方法有 种. 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源:不详 题型:解答题
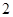 名男生,
名男生,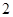 名女生,第二组有
名女生,第二组有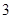 名男生,
名男生,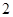 名女生.现在班主任老师要从第一组选出
名女生.现在班主任老师要从第一组选出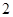 人,从第二组选出
人,从第二组选出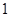 人,请他们在班会上和全班同学分享学习心得.
人,请他们在班会上和全班同学分享学习心得.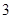 人均是男生的概率;
人均是男生的概率;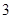 人中有男生也有女生的概率.
人中有男生也有女生的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.720种 | B.520种 | C.600种 | D.360种 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.1860 | B.1320 | C.1140 | D.1020 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.36 | B.72 | C.84 | D.108 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.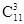 种 种 | B.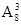 种 种 | C.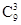 种 种 | D.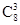 种 种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com