
2013年某市某区高考文科数学成绩抽样统计如下表:
(1)求出表中m、n、M、N的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;(纵坐标保留了小数点后四位小数)
(2)若2013年北京市高考文科考生共有20000人,试估计全市文科数学成绩在90分及90分以上的人数;
(3)香港某大学对内地进行自主招生,在参加面试的学生中,有7名学生数学成绩在140分以上,其中男生有4名,要从7名学生中录取2名学生,求其中恰有1名女生被录取的概率.
(1)M=1000,m=436,n=0.436,N=0.220,频率分布直方图详见试题解析;
(2)全市文科数学成绩在90及90分以上的人数为13120;
(3)7人中录取2人恰有1人为女生的概率为 .
.
解析试题分析:(1)由表格容易求出m、n、M、N的值,频率分布直方图详见试题解析;
(2)由古典概型可以求出全市文科数学成绩在90及90分以上的人数为13120;
(3)设4名男生分别表示为A1、A2、A3、A4,3名女生分别表示为B1、B2、B3,列举出从7名学生中录取2名学生的基本事件有21种,满足条件的有12种,因此7人中录取2人恰有1人为女生的概率为 .
.
试题解析:(1)如图

 ,则M=1000,m=436,n=0.436,N=0.220. 5分
,则M=1000,m=436,n=0.436,N=0.220. 5分
(2)设全市文科数学成绩在90及90分以上的人数为x,则 ,x=13120. 7分
,x=13120. 7分
(3)设4名男生分别表示为A1、A2、A3、A4,3名女生分别表示为B1、B2、B3则从7名学生中录取2名学生的基本事件有:
(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A1,B3),
(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A2,B3),(A3,A4),
(A3,B1),(A3,B2),(A3,B3),(A4,B1),(A4,B2),(A4,B3),
(B1,B2),(B1,B3),(B2,B3),共21种.
设“选2人恰有1名女生”为事件A,有:
(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),(A2,B3),
(A3,B1),(A3,B2),(A3,B3),(A4,B1),(A4,B2),(A4,B3),
共12种,
则 .
.
故7人中录取2人恰有1人为女生的概率为 . 9分
. 9分
考点:频率分布直方图、古典概型.


科目:高中数学 来源: 题型:解答题
从一批苹果中,随机抽取50个,其重量(单位:g)的频数分布表如下:
| 分组(重量) | [80,85) | [85,90) | [90,95) | [95,100) |
| 频数(个) | 5 | 10 | 20 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校高一年级 名学生参加数学竞赛,成绩全部在
名学生参加数学竞赛,成绩全部在 分至
分至 分之间,现将成绩分成以下
分之间,现将成绩分成以下 段:
段:
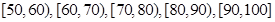 ,据此绘制了如图所示的频率分布直方图.
,据此绘制了如图所示的频率分布直方图. 
(1)求成绩在区间 的频率;
的频率;
(2)从成绩大于等于 分的学生中随机选
分的学生中随机选 名学生,其中成绩在
名学生,其中成绩在 内的学生人数为
内的学生人数为 ,求
,求 的分布列与均值.
的分布列与均值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种报纸,进货商当天以每份1元从报社购进,以每份2元售出.若当天卖不完,剩余报纸报社以每份0.5元的价格回收.根据市场统计,得到这个季节的日销售量X(单位:份)的频率分布直方图(如图所示),将频率视为概率.
(1)求频率分布直方图中a的值;
(2)若进货量为n(单位:份),当n≥X时,求利润Y的表达式;
(3)若当天进货量n=400,求利润Y的分布列和数学期望E(Y)(统计方法中,同一组数据常用该组区间的中点值作为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
经销商经销某种农产品,在一个销售季度内,每售出 t该产品获利润
t该产品获利润 元,未售出的产品,每
元,未售出的产品,每 t亏损
t亏损 元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示。经销商为下一个销售季度购进了
元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示。经销商为下一个销售季度购进了 t该农产品,以
t该农产品,以 (单位:t,
(单位:t, )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, (单位:元)表示下一个销售季度内销商该农产品的利润。
(单位:元)表示下一个销售季度内销商该农产品的利润。
(1)将 表示为
表示为 的函数;(2)根据直方图估计利润
的函数;(2)根据直方图估计利润 不少于57000元的概率.
不少于57000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某班同学利用寒假进行社会实践,对年龄在 的人群随机抽取
的人群随机抽取 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:

(1)补全频率分布直方图,并求 的值;
的值;
(2)从年龄在 的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在
的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对某校高一年级学生参加社区服务次数进行统计,随机抽取了M名学生作为样本,得到这M名学生参加社区服务的次数,根据数据作出了频数的统计如下:
| 分组 | 频数 | 频率 |
| [10,15) | 9 | 0.45 |
| [15,20) | 5 | n |
| [20,25) | m | r |
| [25,30) | 2 | 0.1 |
| 合计 | M | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
(I)估计这次测试数学成绩的平均分;
(II)假设在[90,100]段的学生的数学成绩都不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数中任意抽取2个数,有放回地抽取了3次,记这3次抽取中,恰好是两个学生的数学成绩的次数为 ,求
,求 的分布列及数学期望
的分布列及数学期望 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某高校从今年参加自主招生考试的学生中随机抽取容量为 的学生成绩样本,得到频率分布表如下:
的学生成绩样本,得到频率分布表如下:
| 组数 | 分组 | 频数 | 频率 |
| 第一组 | [230,235) | 8 | 0.16 |
| 第二组 | [235,240) |  | 0.24 |
| 第三组 | [240,245) | 15 |  |
| 第四组 | [245,250) | 10 | 0.20 |
| 第五组 | [250,255] | 5 | 0.10 |
| 合计 |  | 1.00 | |
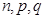 的值;
的值;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com