
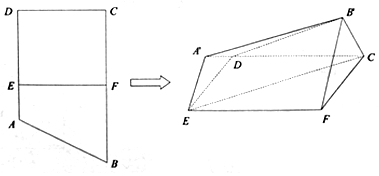
分析 (I)如图所示,取FB′的中点M,连接CM,A′M.可得四边形A′EMB′是平行四边形.A′B′∥EM.同理可得A′D∥CM,可得平面EMC∥平面A′DB′,即可证明CE∥面A′DB′.
(II)取DE的中点O,建立如图所示的空间直角坐标系.∠A′ED=∠B′FC=60°.平面EFCD的一个法向量为$\overrightarrow{n}$=(0,0,1).可得$cos<\overrightarrow{{A}^{′}{B}^{′}},\overrightarrow{n}>$=$\frac{\overrightarrow{{A}^{′}{B}^{′}}•\overrightarrow{n}}{|\overrightarrow{{A}^{′}{B}^{′}}||\overrightarrow{n}|}$.可得直线A′B′与平面FECD所成角的正弦值=|$cos<\overrightarrow{{A}^{′}{B}^{′}},\overrightarrow{n}>$|.
解答 (I)证明:如图所示,取FB′的中点M,连接CM,A′M.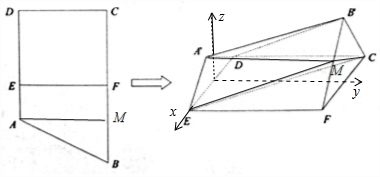
∵A′E$\underset{∥}{=}$B′M,
∴四边形A′EMB′是平行四边形.
∴A′B′∥EM.
∵A′M$\underset{∥}{=}$CD,
∴四边形A′MCD是平行四边形,
∴A′D∥CM,
又∵CM∩EM=M,A′B′∩A′D=A′,
∴平面EMC∥平面A′DB′,
由CE?平面CME.
∴CE∥面A′DB′.
(II)解:取DE的中点O,建立如图所示的空间直角坐标系.∠A′ED=∠B′FC=60°.
则${B}^{′}(0,2,\sqrt{3})$,A′$(\frac{1}{2},0,\frac{\sqrt{3}}{2})$,$\overrightarrow{{A}^{′}{B}^{′}}$=$(\frac{1}{2},-2,-\frac{\sqrt{3}}{2})$.
平面EFCD的一个法向量为$\overrightarrow{n}$=(0,0,1).
∴$cos<\overrightarrow{{A}^{′}{B}^{′}},\overrightarrow{n}>$=$\frac{\overrightarrow{{A}^{′}{B}^{′}}•\overrightarrow{n}}{|\overrightarrow{{A}^{′}{B}^{′}}||\overrightarrow{n}|}$=$\frac{\frac{-\sqrt{3}}{2}}{\sqrt{\frac{1}{4}+4+\frac{3}{4}}×1}$=-$\frac{\sqrt{15}}{10}$.
∴直线A′B′与平面FECD所成角的正弦值=|$cos<\overrightarrow{{A}^{′}{B}^{′}},\overrightarrow{n}>$|=$\frac{\sqrt{15}}{10}$.
点评 本题考查了面面平行的判定定理与性质定理、平行四边形的判定与性质、线面角、数量积运算性质、直角三角形的边角关系、法向量的应用,考查了空间想象能力、推理能力与计算能力,属于中档题.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①④ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{9\sqrt{2}}}{2}$ | B. | $\frac{{9\sqrt{2}}}{4}$ | C. | $\frac{{9\sqrt{2}}}{8}$ | D. | $\frac{{2\sqrt{2}}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a∥b,b∥α,则a∥α | B. | a⊥b,b⊥α,则a∥α | C. | 若a∥b,b⊥α,则a⊥α | D. | 若a⊥b,b∥α,则a⊥α |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com