
【题目】某商品上市30天内每件的销售价格![]() 元与时间
元与时间![]() 天函数关系是
天函数关系是
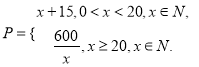 该商品的日销售量
该商品的日销售量![]() 件与时间
件与时间![]() 天函数关系是
天函数关系是
![]() .(1)求该商品上市第20天的日销售金额;
.(1)求该商品上市第20天的日销售金额;
(2)求这个商品的日销售金额的最大值.
【答案】(1)750;(2)第15天时,这个商品的日销售金额最大,最大值为900元.
【解析】试题分析:(1)每件的销售价格![]() 元与时间
元与时间![]() 天函数关系是
天函数关系是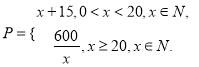 ,
,
则上市20天,根据上述表达式可得日销售量为25,第20天的日销售金额是30×25=750元,即可得到结果。(2)根据题干知日销售金额的表达式分: ![]() ,
, ![]() 时,
时, ![]() =
=![]() ,
, ![]() ,
, ![]() 时,
时, ![]() =
=![]() ,
,
分别求最值即可。
(1)该产品上市第20天的销售价格为30元,日销售量为25件 ,
所以该商品上市第20天的日销售金额是30×25=750元
(2)日销售金额为y元,则y=QP
当![]() ,
, ![]() 时,
时,
![]() =
=![]() ,
,
所以当x=15时,y取得的最大值为900元;
当![]() ,
, ![]() 时,
时,
![]() =
=![]() ,
,
所以当x=20时,y取得的最大值为750元,
综上第15天时,这个商品的日销售金额最大,最大值为900元


科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的方程为x﹣y+4=0,曲线C的参数方程为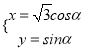 .
.
(1)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为![]() ,判断点P与直线l的位置关系;
,判断点P与直线l的位置关系;
(2)设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某权威机构发布了2014年度“城市居民幸福排行榜”,某市成为本年度城市最“幸福城”.随后,该市某校学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):

(1)指出这组数据的众数和中位数;
(2)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记![]() 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
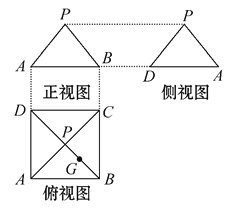
(1)根据三视图,画出该几何体的直观图.
(2)在直观图中,①证明:PD∥平面AGC;
②证明:平面PBD⊥平面AGC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABCA1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,AA1=12,点D是AB的中点.
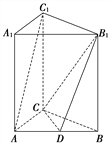
(1)求证:AC⊥B1C;
(2)求证:AC1∥平面CDB1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了了解![]() 两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
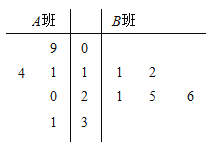
(1)分别求出图中所给两组样本数据的平均值,并据此估计哪个班的学生平均观看的时间较长;
(2)从![]() 班的样本数据中随机抽取一个不超过19的数据记为
班的样本数据中随机抽取一个不超过19的数据记为![]() ,从
,从![]() 班的样本数据中随机抽取一个不超过21的数据记为
班的样本数据中随机抽取一个不超过21的数据记为![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂今年1月、2月、3月生产某种产品的数量分别是1万件、2万件、1.3万件,为了预测以后每个月的产量,以这三个月的产品数量为依据,用一个函数模拟该产品的月产量y与月份x的关系,模拟函数可以选用二次函数或函数y=abx+c(其中a,b,c为常数),已知4月份该产品的产量为1.37万件,请问用以上哪个函数作为模拟函数较好?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电动小汽车生产企业,年利润![]() (出厂价
(出厂价![]() 投入成本)
投入成本)![]() 年销售量.已知上年度生产电动小汽车的投入成本为
年销售量.已知上年度生产电动小汽车的投入成本为![]() 万元/辆,出厂价为
万元/辆,出厂价为![]() 万/辆,年销售量为
万/辆,年销售量为![]() 辆,本年度为打造绿色环保电动小汽车,提高产品档次,计划增加投入成本,若每辆电动小汽车投入成本增加的比例为
辆,本年度为打造绿色环保电动小汽车,提高产品档次,计划增加投入成本,若每辆电动小汽车投入成本增加的比例为![]() (
(![]() ),则出厂价相应提高的比例为
),则出厂价相应提高的比例为![]() .同时年销售量增加的比例为
.同时年销售量增加的比例为![]() .
.
(1)写出本年度预计的年利润![]() (万元)与投入成本增加的比例
(万元)与投入成本增加的比例![]() 的函数关系式;
的函数关系式;
(2)为了使本年度的年利润最大,每辆车投入成本增加的比例应为多少?最大年利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com