
【题目】如图,关于正方体ABCD﹣A1B1C1D1 , 下面结论错误的是( ) 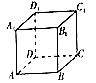
A.BD⊥平面ACC1A1
B.AC⊥BD
C.A1B∥平面CDD1C1
D.该正方体的外接球和内接球的半径之比为2:1
【答案】D
【解析】解:由正方体ABCD﹣A1B1C1D1 , 知: 在A中,∵BD⊥AC,BD⊥AA1 , AC∩AA1=A,∴BD⊥平面ACC1A1 , 故A正确;
在B中,∵ABCD是正方形,∴AC⊥BD,故B正确;
在C中,∵A1B∥D1C,A1B平面CDD1C1 , D1C平面CDD1C1 , 故A1B∥平面CDD1C1 , 故C正确;
在D中,该正方体的外接球和内接球的半径之比为 ![]() =
= ![]() :1.故D错误.
:1.故D错误.
故选:D.
在A中,由BD⊥AC,BD⊥AA1 , 知BD⊥平面ACC1A1;在B中,由ABCD是正方形,知AC⊥BD;在C中,由A1B∥D1C,知A1B∥平面CDD1C1;在D中,该正方体的外接球和内接球的半径之比为 ![]() :1.
:1.


科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ) 当a=0时,求曲线f(x)在x =1处的切线方程;
(Ⅱ) 设函数![]() ,求函数h(x)的极值;
,求函数h(x)的极值;
(Ⅲ) 若![]() 在[1,e](e=2.718 28…)上存在一点x0,使得
在[1,e](e=2.718 28…)上存在一点x0,使得![]() 成立,求a的取值范围.
成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C焦点在y轴上,离心率为 ![]() ,上焦点到上顶点距离为2﹣
,上焦点到上顶点距离为2﹣ ![]() .
.
(1)求椭圆C的标准方程;
(2)直线l与椭圆C交与P,Q两点,O为坐标原点,△OPQ的面积S△OPQ=1,则| ![]() |2+|
|2+| ![]() |2是否为定值,若是求出定值;若不是,说明理由.
|2是否为定值,若是求出定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos4x﹣2sinxcosx﹣sin4x.
(1)求f(x)的最小正周期;
(2)求f(x)的单调增区间;
(3)若 ![]() ,求f(x)的值域.
,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列结论: ①已知函数f(x)是定义在R上的奇函数,若f(﹣1)=2,f(﹣3)=﹣1,则f(3)<f(﹣1);
②函数y=log ![]() (x2﹣2x)的单调递增减区间是(﹣∞,0);
(x2﹣2x)的单调递增减区间是(﹣∞,0);
③已知函数f(x)是奇函数,当x≥0时,f(x)=x2 , 则当x<0时,f(x)=﹣x2;
④若函数y=f(x)的图象与函数y=ex的图象关于直线y=x对称,则对任意实数x,y都有f(xy)=f(x)+f(y).
则正确结论的序号是(请将所有正确结论的序号填在横线上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是二次函数,方程f(x)=0有两相等实根,且f′(x)=2x+2
(1)求f(x)的解析式.
(2)求函数y=f(x)与y=﹣x2﹣4x+1所围成的图形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com