
【题目】某工厂为了对新研发的一种产品进行合理定价,将该定价按事先拟定的价格进行试销,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程![]() ;
;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?
附:  .
.
 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,已知点![]() ,圆
,圆![]()
(I)在极坐标系中,以极点为原点,极轴为![]() 轴正半轴建立平面直角坐标系,取相同的长度单位,求圆
轴正半轴建立平面直角坐标系,取相同的长度单位,求圆![]() 的直角坐标方程;
的直角坐标方程;
(II)求点![]() 到圆
到圆![]() 圆心的距离.
圆心的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据:
(吨标准煤)的几组对照数据:
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
(1)已知产量![]() 和能耗
和能耗![]() 呈线性关系,请根据上表提供的数据,用最小二乘法求出
呈线性关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产耗能为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式: 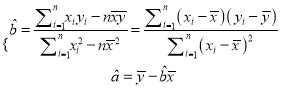
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校课题组为了研究学生的数学成绩与学生细心程度的关系,在本校随机调查了100名学生进行研究.研究结果表明:在数学成绩及格的60名学生中有45人比较细心,另外15人比较粗心;在数学成绩不及格的40名学生中有10人比较细心,另外30人比较粗心.
(1)试根据上述数据完成![]() 列联表;
列联表;
数学成绩及格 | 数学成绩不及格 | 合计 | |
比较细心 | 45 | ||
比较粗心 | |||
合计 | 60 | 100 |
(2)能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系?
参考数据:独立检验随机变量![]() 的临界值参考表:
的临界值参考表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在各棱长为![]() 的直四棱柱
的直四棱柱![]() 中,底面
中,底面![]() 为棱形,
为棱形, ![]() 为棱
为棱![]() 上一点,且
上一点,且![]()
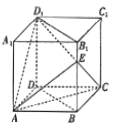
(1)求证:平面![]() 平面
平面![]() ;
;
(2)平面![]() 将四棱柱
将四棱柱![]() 分成上、下两部分,求这两部分的体积之比.
分成上、下两部分,求这两部分的体积之比.
(棱台的体积公式为![]() ,其中
,其中![]() 分别为上、下底面面积,
分别为上、下底面面积, ![]() 为棱台的高)
为棱台的高)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com