
【题目】已知函数f(x)是定义在R上的奇函数,且当x<0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象如图所示,

(1)画出函数f(x),x∈R剩余部分的图象,并根据图象写出函数f(x),x∈R的单调区间;(只写答案)
(2)求函数f(x),x∈R的解析式.
【答案】(1)图象见解析;递减区间为(﹣∞,﹣1],[1,+∞);增区间为(﹣1,1);
(2)f(x)![]() .
.
【解析】
(1)根据题意,由奇函数的性质结合函数f(x)在y轴左侧的图象,即可补充函数图象,据此写出函数的单调区间即可得答案;
(2)根据题意,由奇函数的性质可得f(0)=0,设x>0时,则﹣x<0,由函数的解析式可得f(﹣x),结合奇函数的性质可得f(x)的解析式,综合即可得答案.
(1)根据题意,函数f(x)是定义在R上的奇函数,则其图象如图:
其递减区间为(﹣∞,﹣1],[1,+∞);
增区间为(﹣1,1);
(2)根据题意,函数f(x)是定义在R上的奇函数,则f(0)=0,满足f(x)=x2+2x;
当x>0时,则﹣x<0,则f(﹣x)=(﹣x)2+2(﹣x)=x2﹣2x,
又由函数f(x)是定义在R上的奇函数,则f(x)=﹣f(﹣x)=﹣x2+2x,
综上:f(x)![]() .
.
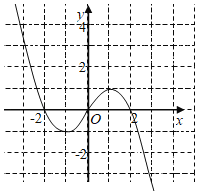


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD= ![]() ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB. 
(1)求PA的长;
(2)求二面角B﹣AF﹣D的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018河南安阳市高三一模】如下图,在平面直角坐标系![]() 中,直线
中,直线![]() 与直线
与直线![]() 之间的阴影部分即为
之间的阴影部分即为![]() ,区域
,区域![]() 中动点
中动点![]() 到
到![]() 的距离之积为1.
的距离之积为1.

(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)动直线![]() 穿过区域
穿过区域![]() ,分别交直线
,分别交直线![]() 于
于![]() 两点,若直线
两点,若直线![]() 与轨迹
与轨迹![]() 有且只有一个公共点,求证:
有且只有一个公共点,求证: ![]() 的面积恒为定值.
的面积恒为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2+bx+c有两个零点1和﹣1.
(1)求f(x)的解析式;
(2)设g(x)![]() ,试判断函数g(x)在区间(﹣1,1)上的单调性并用定义证明;
,试判断函数g(x)在区间(﹣1,1)上的单调性并用定义证明;
(3)由(2)函数g(x)在区间(﹣1,1)上,若实数t满足g(t﹣1)﹣g(﹣t)>0,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)=a![]() (a为常数).
(a为常数).
(1)求a的值;
(2)若函数g(x)=|(2x+1)f(x)|﹣k有2个零点,求实数k的取值范围;
(3)若x∈[﹣2,﹣1]时,不等式f(x)![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只药用昆虫的产卵数y与一定范围内的温度x有关, 现收集了该种药用昆虫的6组观测数据如下表:
温度x/C | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数y/个 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算得: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,线性回归模型的残差平方和
,线性回归模型的残差平方和![]() ,e8.0605≈3167,其中xi, yi分别为观测数据中的温度和产卵数,i=1, 2, 3, 4, 5, 6.
,e8.0605≈3167,其中xi, yi分别为观测数据中的温度和产卵数,i=1, 2, 3, 4, 5, 6.
(Ⅰ)若用线性回归模型,求y关于x的回归方程![]() =
=![]() x+
x+![]() (精确到0.1);
(精确到0.1);
(Ⅱ)若用非线性回归模型求得y关于x的回归方程为![]() =0.06e0.2303x,且相关指数R2=0.9522.
=0.06e0.2303x,且相关指数R2=0.9522.
( i )试与(Ⅰ)中的回归模型相比,用R2说明哪种模型的拟合效果更好.
( ii )用拟合效果好的模型预测温度为35C时该种药用昆虫的产卵数(结果取整数).
附:一组数据(x1,y1), (x2,y2), ...,(xn,yn ), 其回归直线![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为

![]() =
=![]()
![]() ;相关指数R2=
;相关指数R2= .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个结论:
①函数![]() 是偶函数;
是偶函数;
②当![]() 时,函数
时,函数![]() 的值域是
的值域是![]() ;
;
③若扇形的周长为![]() ,圆心角为
,圆心角为![]() ,则该扇形的弧长为6 cm;
,则该扇形的弧长为6 cm;
④已知定义域为![]() 的函数
的函数![]() ,当且仅当
,当且仅当![]() 时,
时,![]() 成立.
成立.
则上述结论中正确的是______(写出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:
(单位:![]() )的影响,对近
)的影响,对近![]() 年的年宣传费
年的年宣传费![]() 和年销售量
和年销售量![]() 作了初步统计和处理,得到的数据如下:
作了初步统计和处理,得到的数据如下:
年宣传费 |
|
|
|
|
年销售量 |
|
|
|
|
![]() ,
,![]() .
.

(1)在给定的坐标系中画出表中数据的散点图;
(2)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若公司计划下一年度投入宣传费![]() 万元,试预测年销售量
万元,试预测年销售量![]() 的值.
的值.
参考公式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com